题目内容
15.在△ABC中,角A、B、C所对的边分别是a、b、c,已知sinB+sinC=msinA(m∈R),且a2-4bc=0.(1)当a=2,$m=\frac{5}{4}$时,求b、c的值;
(2)若角A为锐角,求m的取值范围.
分析 (1)sinB+sinC=msinA(m∈R),利用正弦定理可得:b+c=ma,且a2-4bc=0.a=2,$m=\frac{5}{4}$时,代入解出即可得出.
(2)利用余弦定理、不等式的解法即可得出.
解答 解:(1)由题意得b+c=ma,a2-4bc=0.
当$a=2,m=\frac{5}{4}$时,$b+c=\frac{5}{2}$,bc=1.
解得$\left\{\begin{array}{l}b=2\\ c=\frac{1}{2}\end{array}\right.或\left\{\begin{array}{l}b=\frac{1}{2}\\ c=2\end{array}\right.$.
(2)$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{{{{({b+c})}^2}-2bc-{a^2}}}{2bc}=\frac{{{m^2}{a^2}-\frac{a^2}{2}-{a^2}}}{{\frac{a^2}{2}}}=2{m^2}-3∈(0,1)$.
∴$\frac{3}{2}<{m^2}<2$,又由b+c=ma可得m>0,所以$\frac{{\sqrt{6}}}{2}<m<\sqrt{2}$.
点评 本题考查了正弦定理余弦定理、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.函数f(x)=|x+2017|-|x-2016|的最大值为( )
| A. | -1 | B. | 1 | C. | 4033 | D. | -4033 |
3.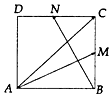 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
7.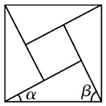 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | 0 |
4.将一根长为10米的木棒截成三段,则每段木棒长不低于1米的概率为( )
| A. | $\frac{8}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{49}{100}$ | D. | $\frac{49}{200}$ |