题目内容
4．函数f（x）=$\sqrt{x-2}$+lg（5-x）的定义域是[2，5）．分析 根据开偶次方根被开方数大于等于0，对数函数的真数大于0，列出不等式组求出定义域．
解答 解：要使函数有意义，只需
$\left\{\begin{array}{l}{x-2≥0}\\{5-x＞0}\end{array}\right.$，
解得2≤x＜5，
∴函数f（x）=$\sqrt{x-2}$+lg（5-x）的定义域是[2，5）．
故答案为：[2，5）．
点评 本题考查了根据函数解析式求定义域的应用问题，是基础题．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
8．若数列{an}的前n项和为Sn，S2n-12+S2n2=4（a2n-2），则2a1+a100=（ ）
| A． | -8 | B． | -6 | C． | 0 | D． | 2 |
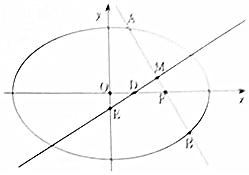过椭圆C：$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A，B两点，M是AB的中点．
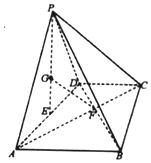如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD为梯形，AB∥CD，AB=2DC=2$\sqrt{3}$，且△PAD与△ABD均为正三角形，E为AD的中点，G为△PAD的重心，AC∩BD=F