题目内容
2.某三棱锥的正视图如图1所示,则在图2①②③④中,所有可能成为这个三棱锥的俯视图的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
分析 根据空间三棱锥的正视图,分别进行验证,即可得出结论.
解答 解:如图1三棱锥C-DEF,
是选项①的模型;
如图2的三棱锥P-ABC,
是选项②的模型;
如图3的三棱锥A-PMN,
是选项③的模型,
如图4的三棱锥B-XYZ,
是选项④的模型;
综上,①②③④都有可能是该三棱锥的俯视图.
故选:D.
点评 本题主要考查空间几何体的三视图的判断,根据选项分别进行验证是解决本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
6.已知复数z=1+cosα+isinα(π<α<2π),则|$\overline{z}$|=( )
| A. | 2cos$\frac{α}{2}$ | B. | -2cos$\frac{α}{2}$ | C. | 2sin$\frac{α}{2}$ | D. | -2sin$\frac{α}{2}$ |
11.已知实数1,t,4成等比数列,则圆锥曲线$\frac{x^2}{t}+{y^2}$=1的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | C. | $\frac{1}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或3 |
12.如图,根据样本的频率分布直方图,估计样本的中位数是( )


| A. | 10 | B. | 12 | C. | 13 | D. | 16 |
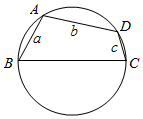 如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.
如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.