题目内容
已知向量
=(3,5),
=(cosα,sinα),且
∥
,则tanα等于( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:直接利用向量共线的坐标表示列式,移项作商得答案.
解答:
解:∵向量
=(3,5),
=(cosα,sinα),且
∥
,
∴3sinα-5cosα=0,
则tanα=
.
故选:B.
| a |
| b |
| a |
| b |
∴3sinα-5cosα=0,
则tanα=
| 5 |
| 3 |
故选:B.
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0.是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
相关题目
方程ay=b2x2+c中的a,b,c∈{-2,-1,0,1,2,3,4},且a,b,c互不相同.在所有这些方程所表示的曲线中,不同的抛物线共有( )
| A、150条 | B、104条 |
| C、100条 | D、62条 |
已知椭圆
+
=1的一个焦点为(2,0),则椭圆的方程是( )
| x2 |
| a2 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
| A、模型1的R2为0.55 |
| B、模型2的R2为0.65 |
| C、模型3的R2为0.79 |
| D、模型4的R2为0.95 |
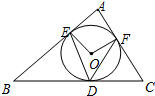 如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A、40° | B、55° |
| C、65° | D、70° |
用二分法求方程lnx+2x=6的近似解(精度0.01),先令f(x)=lnx+2x-6,则根据下表数据,方程的近似解可能是( )
| x | 2 | 3 | 2.5 | 2.75 | 2.625 | 2.5625 | 2.53125 | 2.546875 | 2.5390625 |
| f(x)近似值 | -1.31 | 0.69 | -0.84 | 0.52 | 0.215 | 0.0666 | -0.009 | 0.029 | 0.010 |
| A、2.512 |
| B、2.522 |
| C、2.532 |
| D、2.542 |
执行如图所示的程序框图,如果输出2,那么判断框内应填入的条件是( )


| A、k≤3? | B、k≤4? |
| C、k>3? | D、k>4? |
设a>b>c,k∈R,且(a-c)•(
+
)≥k恒成立,则k的最大值为( )
| 1 |
| a-b |
| 1 |
| b-c |
| A、2 | B、3 | C、4 | D、5 |