题目内容
已知椭圆C：
+
=1（a＞b＞0）的右焦点为F（1，0），经过F与B（0，b）的直线与圆x2+y2=
相切．
（1）求椭圆C的方程；
（2）过点F的直线l交椭圆于M、N两点，求
•
的最值．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
（1）求椭圆C的方程；
（2）过点F的直线l交椭圆于M、N两点，求
| FM |
| FN |
考点：直线与圆锥曲线的关系,圆的切线方程,椭圆的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）经过F与B（0，b）的直线方程为x+
=1，利用经过F与B（0，b）的直线与圆x2+y2=
相切，结合点到直线的距离公式，求出b再求出a，即可得到椭圆C的方程；
（2）设直线l的方程为y=k（x-1），代入椭圆方程，消y并整理，利用向量的数量积公式，结合韦达定理表示出
•
，化简可求最值．
| y |
| b |
| 3 |
| 4 |
（2）设直线l的方程为y=k（x-1），代入椭圆方程，消y并整理，利用向量的数量积公式，结合韦达定理表示出
| FM |
| FN |
解答：
解：（1）经过F与B（0，b）的直线方程为x+
=1．
∵经过F与B（0，b）的直线与圆x2+y2=
相切，
∴圆心到直线的距离d=
=
，
∴b=
，
∵c=1，
∴a=
=2，
∴椭圆C的方程为
+
=1；
（2）可设直线l的方程为y=k（x-1），代入椭圆方程，消y并整理得（4k2+3）x2-8k2x+4k2-12=0．
设M（x1，y1），N（x2，y2），则x1+x2=
，x1x2=
，
△=（-8k2）2-4（4k2+3）（4k2-12）＞0恒成立．
•
=（x1-1，y1）•（x2-1，y2）=（x1-1）（x2-1）+y1y2=（1+k2）[x1x2-（x1+x2）+1]
=（1+k2）（
-
+1）=
，
令1+k2=t（t≥1），则
•
=
=
，
∵t≥1，∴-4＜
-4≤-3，
∴-3≤
•
＜-
即
•
的最小值为-3．
| y |
| b |
∵经过F与B（0，b）的直线与圆x2+y2=
| 3 |
| 4 |
∴圆心到直线的距离d=
| 1 | ||||
|
| ||
| 2 |
∴b=
| 3 |
∵c=1，
∴a=
| b2+c2 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）可设直线l的方程为y=k（x-1），代入椭圆方程，消y并整理得（4k2+3）x2-8k2x+4k2-12=0．
设M（x1，y1），N（x2，y2），则x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
△=（-8k2）2-4（4k2+3）（4k2-12）＞0恒成立．
| FM |
| FN |
=（1+k2）（
| 4k2-12 |
| 4k2+3 |
| 8k2 |
| 4k2+3 |
| -9(1+k2) |
| 4k2+3 |
令1+k2=t（t≥1），则
| FM |
| FN |
| 9t |
| 1-4t |
| 9 | ||
|
∵t≥1，∴-4＜
| 1 |
| t |
∴-3≤
| FM |
| FN |
| 3 |
| 4 |
即
| FM |
| FN |
点评：本题考查直线与圆的位置关系，考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查向量的数量积公式，属于中档题．
练习册系列答案
相关题目
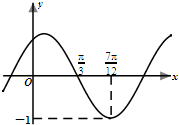已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜