题目内容
已知△ABC中，顶点A（2，2），边AB上的中线CD所在直线的方程是x+y=0，边AC上的高BE所在直线的方程是x+3y+4=0，求BC所在直线．
考点：直线的一般式方程
专题：直线与圆
分析：先由AB的中点公式求出B点的坐标，再由AC与BE的交点求出C点的坐标，从而求出直线BC的方程．
解答：
解：由题意可设B（-3a-4，a），
则AB的中点D（
，
）必在直线CD上，
∴
+
=0，
∴a=0，∴B（-4，0），
又直线AC方程为：
y-2=3（x-2），
即y=3x-4，
由
得，
C（1，-1）．
则BC所在直线为x+5y+4=0．
则AB的中点D（
| -3a-2 |
| 2 |
| a+2 |
| 2 |
∴
| -3a-2 |
| 2 |
| a+2 |
| 2 |
∴a=0，∴B（-4，0），
又直线AC方程为：
y-2=3（x-2），
即y=3x-4，
由
|
C（1，-1）．
则BC所在直线为x+5y+4=0．
点评：本题考查了求直线方程的问题，是基础题．
练习册系列答案
相关题目
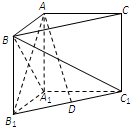如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1．
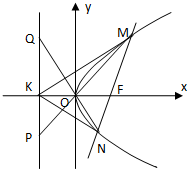如图，已知抛物线y2=4x的焦点为F，过F的直线交抛物线于M、N两点，其准线l与x轴交于K点．