题目内容
对于函数f(x),若存在实数对(a,b),使得f(a+x)•f(a-x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f1(x)=x是否为“(a,b)型函数”,并说明理由;
(2)若函数f2(x)=tanx是“(a,b)型函数”,求满足条件的实数对(a,b)所组成的集合;
(3)已知函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4).当x∈[0,1]时,g(x)=x2+m(x-1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤4,试求实数m的取值范围.
(1)判断函数f1(x)=x是否为“(a,b)型函数”,并说明理由;
(2)若函数f2(x)=tanx是“(a,b)型函数”,求满足条件的实数对(a,b)所组成的集合;
(3)已知函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4).当x∈[0,1]时,g(x)=x2+m(x-1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤4,试求实数m的取值范围.
考点:三角函数中的恒等变换应用,抽象函数及其应用
专题:新定义,函数的性质及应用
分析:(1)根据f(x)是“(a,b)型函数”的定义,判断f1(x)=x中是否存在实数对(a,b),使得等式f(a+x)•f(a-x)=b对定义域中的每一个x都成立,即可得到答案;
(2)根据函数f2(x)=tanx是“(a,b)型函数”,即可得到f(a+x)•f(a-x)=b对定义域中的每一个x都成立,即可得到答案;
(3)根据函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4),根据对称轴与区间的位置关系进行分类讨论,分别求出g(x)在[0,1]和[0,2]上的值域,列出不等式组,求解即可得到m的取值范围.
(2)根据函数f2(x)=tanx是“(a,b)型函数”,即可得到f(a+x)•f(a-x)=b对定义域中的每一个x都成立,即可得到答案;
(3)根据函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4),根据对称轴与区间的位置关系进行分类讨论,分别求出g(x)在[0,1]和[0,2]上的值域,列出不等式组,求解即可得到m的取值范围.
解答:
解:(1)f1(x)=x不是“(a,b)型函数”,
∵f1(x)=x,
∴f1(a+x)=a+x,f1(a-x)=a-x,
∴f1(a+x)•f1(a-x)=(a+x)(a-x)=b,
即a2-x2=b,
∴不存在实数对(a,b)使得a2-x2=b对定义域中的每一个x都成立,
∴f1(x)=x不是“(a,b)型函数”;
(2)∵函数f2(x)=tanx是“(a,b)型函数”,
∴tan(a+x)tan(a-x)=b.
即
?
=
,
∴当tan2a=1,即tana=±1时,
?
=
=1=b,
此时a=±
+kπ,b=1,
∴满足条件的实数对(a,b)所组成的集合(±
+kπ,1),k∈Z.
(3)∵函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4),
∴g(1+x)g(1-x)=4,
∴当x∈[1,2]时,g(x)=
,其中2-x∈[0,1],
又∵x∈[0,1]时,g(x)=x2+m(1-x)+1=x2-mx+m+1,其对称轴方程为x=
,
①当
>1,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],
∴g(x)在[0,2]上的值域为[2,m+1]∪[
,2]=[
,m+1],
由题意,得
,∴2<m≤3;
②当
≤
≤1,即1≤m≤2时,g(x)的值域为[g(
),g(0)],
即[m+1-
,m+1]∪[
,
],
由题意,得
且
,解得1≤m≤2;
③当0<
≤
,即0<m≤1时,g(x)的值域为[g(
),g(1)],
即[m+1-
,2],
∴g(x)在[0,2]上的值域为[m+1-
,2]∪[2,
]=[m+1-
,
],
由题意,得
,解得0<m≤1.
综合①②③,所求m的取值范围是0<m≤3.
∵f1(x)=x,
∴f1(a+x)=a+x,f1(a-x)=a-x,
∴f1(a+x)•f1(a-x)=(a+x)(a-x)=b,
即a2-x2=b,
∴不存在实数对(a,b)使得a2-x2=b对定义域中的每一个x都成立,
∴f1(x)=x不是“(a,b)型函数”;
(2)∵函数f2(x)=tanx是“(a,b)型函数”,
∴tan(a+x)tan(a-x)=b.
即
| tan?a+tan?x |
| 1-tan?atan?x |
| tan?a-tan?x |
| 1+tan?atan?x |
| tan?2a-tan?2x |
| 1-tan?2atan?2x |
∴当tan2a=1,即tana=±1时,
| tan?a+tan?x |
| 1-tan?atan?x |
| tan?a-tan?x |
| 1+tan?atan?x |
| tan?2a-tan?2x |
| 1-tan?2atan?2x |
此时a=±
| π |
| 4 |
∴满足条件的实数对(a,b)所组成的集合(±
| π |
| 4 |
(3)∵函数g(x)是“(a,b)型函数”,对应的实数对(a,b)为(1,4),
∴g(1+x)g(1-x)=4,
∴当x∈[1,2]时,g(x)=
| 4 |
| g(2-x) |
又∵x∈[0,1]时,g(x)=x2+m(1-x)+1=x2-mx+m+1,其对称轴方程为x=
| m |
| 2 |
①当
| m |
| 2 |
∴g(x)在[0,2]上的值域为[2,m+1]∪[
| 4 |
| m+1 |
| 4 |
| m+1 |
由题意,得
|
②当
| 1 |
| 2 |
| m |
| 2 |
| m |
| 2 |
即[m+1-
| m2 |
| 4 |
| 4 |
| m+1 |
| 4 | ||
m+1-
|
由题意,得
|
|
③当0<
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
即[m+1-
| m2 |
| 4 |
∴g(x)在[0,2]上的值域为[m+1-
| m2 |
| 4 |
| 4 | ||
m+1-
|
| m2 |
| 4 |
| 4 | ||
m+1-
|
由题意,得
|
综合①②③,所求m的取值范围是0<m≤3.
点评:本题考查了函数与方程的综合应用.函数的零点与方程根的关系.函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.解题的关键是将方程问题转化成函数的问题进行求解.难度较大.

练习册系列答案
相关题目
已知椭圆
+y2=1,则该椭圆的离心率为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.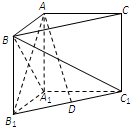 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.