题目内容
给定实数a>1,求函数f(x)=
的最小值.
| (a+sinx)(4+sinx) |
| 1+sinx |
考点:三角函数的最值
专题:计算题,函数的性质及应用
分析:化简f(x)=
=1+sinx+
+a+2,对a分1<a≤
与a>
讨论,利用基本不等式与双钩函数的性质即可求得函数f(x)=
的最小值.
| (a+sinx)(4+sinx) |
| 1+sinx |
| 3(a-1) |
| 1+sinx |
| 7 |
| 3 |
| 7 |
| 3 |
| (a+sinx)(4+sinx) |
| 1+six |
解答:
解:f(x)=
=1+sinx+
+a+2.
当1<a≤
时,0<
≤2,
此时f(x)=1+sinx+
+a+2≥2
+a+2,
且当sinx=
-1∈(-1,1])时不等式等号成立,
故f(x)min=2
+a+2;
当a>
时,
>2,此时“双钩”函数
y=t+
在(0,
]内是递减,
故此时fmin(x)=f(1)=2+
+a+2=
.
综上所述,fmin(x)=
.
| (a+sinx)(4+sinx) |
| 1+sinx |
| 3(a-1) |
| 1+sinx |
当1<a≤
| 7 |
| 3 |
| 3(a-1) |
此时f(x)=1+sinx+
| 3(a-1) |
| 1+sinx |
| 3(a-1) |
且当sinx=
| 3(a-1) |
故f(x)min=2
| 3(a-1) |
当a>
| 7 |
| 3 |
| 3(a-1) |
y=t+
| 3(a-1) |
| t |
| 3(a-1) |
故此时fmin(x)=f(1)=2+
| 3(a-1) |
| 2 |
| 5(a+1) |
| 2 |
综上所述,fmin(x)=
|
点评:本题考查三角函数的最值,着重考查基本不等式与双钩函数的性质,考查转化思想与分类讨论思想的综合应用,属于难题.

练习册系列答案
相关题目
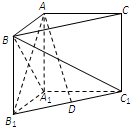 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.