题目内容
已知等腰△ABC中,AB=BC=2,∠ACB=120°,△ABC所在平面外一点P到△ABC三顶点的距离相等且为4,求直线PC与平面ABC所成角的大小.
考点:直线与平面所成的角
专题:计算题,空间角
分析:P是△ABC所在平面外一点,O是P点在平面a上的射影,证明O是△ABC的外心,求出AO,即可求出直线PC与平面ABC所成角的大小.
解答:
 解:如图P是△ABC所在平面外一点,O是P点在平面a上的射影,则∠PCO为直线PC与平面ABC所成角.
解:如图P是△ABC所在平面外一点,O是P点在平面a上的射影,则∠PCO为直线PC与平面ABC所成角.
若P到△ABC三个顶点的距离相等,
故△POA≌△POB≌△POC
故OA=OB=OC,
由三角形外心的定义知此时点O是三角形的外心,
等腰△ABC中,AC=BC=2,∠ACB=120°,
∴AB=2
,
∵P到△ABC三顶点的距离相等且为4,
∴AO=2,
∴sin∠PCO=
=
,
∴∠PCO=30°.
 解:如图P是△ABC所在平面外一点,O是P点在平面a上的射影,则∠PCO为直线PC与平面ABC所成角.
解:如图P是△ABC所在平面外一点,O是P点在平面a上的射影,则∠PCO为直线PC与平面ABC所成角.若P到△ABC三个顶点的距离相等,
故△POA≌△POB≌△POC
故OA=OB=OC,
由三角形外心的定义知此时点O是三角形的外心,
等腰△ABC中,AC=BC=2,∠ACB=120°,
∴AB=2
| 3 |
∵P到△ABC三顶点的距离相等且为4,
∴AO=2,
∴sin∠PCO=
| 2 |
| 4 |
| 1 |
| 2 |
∴∠PCO=30°.
点评:本题考查三角形内的特殊点内心,外心,垂心,考查点、线、面间的距离,考查学生计算能力,逻辑思维能力,是基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
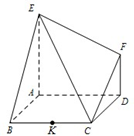 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
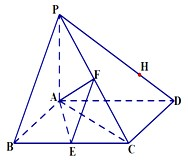 四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.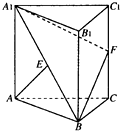 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点. 如图,在三棱柱ABC-A1B1C中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.
如图,在三棱柱ABC-A1B1C中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.