题目内容
线段a∥平面α,a与平面α相距4cm,平面α内有直线b与c相距6cm,且a∥b,若a和b相距5cm,则a和c相距 cm.
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:先根据题意将空间几何问题转化为平面几何问题解决.即作一个平面β,使得a,b,c都垂直于β,且平面β与a,b,c分别相交于A,B,C.如图,下面只要在平面图形ABC中解决即可.最后利用解三角形知识即可求得AC即直线a,c之间的距离.
解答:
解:由题意,a∥b∥c,作一个平面β,使得a,b,c都垂直于β,且平面β与a,b,c分别相交于A,B,C.如图.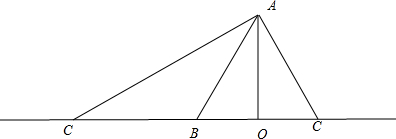
其中:AO=4,AB=5,BC=6,
在三角形AOC中,AC=
=
=5,
或者:AC=
=
.
故答案为5或

其中:AO=4,AB=5,BC=6,
在三角形AOC中,AC=
| AO2+OC2 |
| 16+9 |
或者:AC=
| 16+81 |
| 97 |
故答案为5或
| 97 |
点评:本题主要考查了点、线、面间的距离计算、转化能力,以及空间几何体的概念、空间想象力,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若函数f(x)满足f(x)+1=
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,方程f(x)-mx-2m=0有两个实数解,则实数m的取值范围是( )
| 1 |
| f(x+1) |
A、0<m≤
| ||
B、0<m<
| ||
C、
| ||
D、
|
已知集合A={x|-1<x<1},则下列选项中正确的是( )
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |
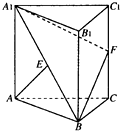 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点. 某少数民族的刺绣有着悠久的历史,如图所示为她们刺绣最简单的三个图案,这些图案都是由小圆构成,小圆数越多刺绣越漂亮.现按同样的规律刺绣(小圆的摆放规律相同),设第n个图形包含f(n)个小圆.则f(5)的值为
某少数民族的刺绣有着悠久的历史,如图所示为她们刺绣最简单的三个图案,这些图案都是由小圆构成,小圆数越多刺绣越漂亮.现按同样的规律刺绣(小圆的摆放规律相同),设第n个图形包含f(n)个小圆.则f(5)的值为