题目内容
已知函数f（x）=x3+ax2+bx（a，b∈R）的图象过点P（1，f（1）），且在点P处的切线方程为8x-y-6=0．
（1）求a，b的值；
（2）求函数y=f（x）的单调区间．
（1）求a，b的值；
（2）求函数y=f（x）的单调区间．
考点：利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：（1）由题意得方程组解出a，b的值即可，（2）先求出函数的导数，解不等式，即可求出单调区间．
解答：
解：（1）因为点P在切线上，
所以8-f（1）-6=0，即f（1）=2．
即有2=1+a+b，化简得a+b①，
又因为函数图象在P点处切线的斜率为8，
所以f'（1）=8，
因为f'（x）=3x2+2ax+b，
所以8=3+2a+b，化简得2a+b②，
联立①、②解得a=4，b=-3．
（2）由（1）得f（x）=x3+4x2-3x，
所以f'（x）=3x2+8x-3，
由f'（x）＞0得x＜-3，或x＞
．
由f'（x）＜0得-3＜x＜
．
所以函数f（x）的单调递增区间为（-∞，-3），(
，+∞)；
单调递减区间为(-3，
)．
所以8-f（1）-6=0，即f（1）=2．
即有2=1+a+b，化简得a+b①，
又因为函数图象在P点处切线的斜率为8，
所以f'（1）=8，
因为f'（x）=3x2+2ax+b，
所以8=3+2a+b，化简得2a+b②，
联立①、②解得a=4，b=-3．
（2）由（1）得f（x）=x3+4x2-3x，
所以f'（x）=3x2+8x-3，
由f'（x）＞0得x＜-3，或x＞
| 1 |
| 3 |
由f'（x）＜0得-3＜x＜
| 1 |
| 3 |
所以函数f（x）的单调递增区间为（-∞，-3），(
| 1 |
| 3 |
单调递减区间为(-3，
| 1 |
| 3 |
点评：本题考察了函数的单调性，切线的方程，导数的应用，是一道基础题．
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目
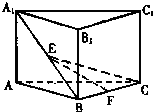如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
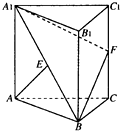如图，三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC，△ABC为等边三角形，侧面AA1C1C是正方形，E是A1B的中点，F是棱CC1上的点．
如图，在三棱柱ABC-A1B1C中，AA1⊥底面ABC，AB⊥AC，AC=AA1，E、F分别是棱BC、CC1的中点．
某少数民族的刺绣有着悠久的历史，如图所示为她们刺绣最简单的三个图案，这些图案都是由小圆构成，小圆数越多刺绣越漂亮．现按同样的规律刺绣（小圆的摆放规律相同），设第n个图形包含f（n）个小圆．则f（5）的值为