题目内容
已知正项数列{an}的前n项和为Sn,且对一切n∈N+,a13+a23+…+an3=Sn2;
(1)求a1,a2,a3的值;
(2)求数列{an}的通项公式an;
(3)若bn=2n+(-1)nm•an是递增数列,求实数m的取值范围.
(1)求a1,a2,a3的值;
(2)求数列{an}的通项公式an;
(3)若bn=2n+(-1)nm•an是递增数列,求实数m的取值范围.
考点:数列与函数的综合,数列的函数特性,数列的求和
专题:等差数列与等比数列
分析:(1)利用已知条件通过n=1,2,3,即可求a1,a2,a3的值;
(2)写出
+
+…+
+
=
,通过作差,推出an+1-an=1(n≥2),然后求数列{an}的通项公式an;
(3)化简bn=2n+(-1)nm•an表达式,利用递增数列,得到m的不等式,通过构造函数然后求实数m的取值范围.
(2)写出
| a | 3 1 |
| a | 3 2 |
| a | 3 n |
| a | 3 n+1 |
| S | 2 n+1 |
(3)化简bn=2n+(-1)nm•an表达式,利用递增数列,得到m的不等式,通过构造函数然后求实数m的取值范围.
解答:
解:(1)∵an>0,令n=1得,
=
=
⇒a1=1
令n=2得,
+
=
⇒1+
=(1+a2)2⇒a2=2
令n=3得,
+
+
=
⇒1+8+
=(3+a3)2⇒a3=3
(2)
+
+…+
=
…①
+
+…+
+
=
…②
由②-①:
=
-
=(Sn+1-Sn)(Sn+1+Sn)=an+1(Sn+1+Sn)
∴
=Sn+1+Sn,
=Sn+Sn-1(n≥2)
∴
-
=an+1+an⇒an+1-an=1(n≥2)
又a2-a1=1,
∴{an}是首项为1,公差为1的等差数列
∴an=n(n∈N+)
(3)由(2)得:bn=2n+(-1)nm•n,又{bn}是递增数列,
即:bn<bn+1(n∈N+)恒成立;
当n=2k(k∈N+)时,bn<bn+1(n∈N+)?m<
(k∈N+)恒成立,
设ck=
,ck+1-ck=
>0⇒ck<ck+1⇒m<
;
同理,当n=2k-1(k∈N+)时,bn<bn+1(n∈N+)恒成立?m>-
(k∈N+)?m>-
;
综上可得:m∈(-
,
)
| a | 3 1 |
| S | 2 1 |
| a | 2 1 |
令n=2得,
| a | 3 1 |
| a | 3 2 |
| S | 2 2 |
| a | 3 2 |
令n=3得,
| a | 3 1 |
| a | 3 2 |
| a | 3 3 |
| S | 2 3 |
| a | 3 3 |
(2)
| a | 3 1 |
| a | 3 2 |
| a | 3 n |
| S | 2 n |
| a | 3 1 |
| a | 3 2 |
| a | 3 n |
| a | 3 n+1 |
| S | 2 n+1 |
由②-①:
| a | 3 n+1 |
| S | 2 n+1 |
| S | 2 n |
∴
| a | 2 n+1 |
| a | 2 n |
∴
| a | 2 n+1 |
| a | 2 n |
又a2-a1=1,
∴{an}是首项为1,公差为1的等差数列
∴an=n(n∈N+)
(3)由(2)得:bn=2n+(-1)nm•n,又{bn}是递增数列,
即:bn<bn+1(n∈N+)恒成立;
当n=2k(k∈N+)时,bn<bn+1(n∈N+)?m<
| 4k |
| 4k+1 |
设ck=
| 4k |
| 4k+1 |
| 4k(12k-1) |
| (4k+1)(4k+5) |
| 4 |
| 5 |
同理,当n=2k-1(k∈N+)时,bn<bn+1(n∈N+)恒成立?m>-
| 4k |
| 2(4k-1) |
| 2 |
| 3 |
综上可得:m∈(-
| 2 |
| 3 |
| 4 |
| 5 |
点评:本题考查数列与函数的综合应用,数列的通项公式的求法,考查恒成立的知识,考查分析问题解决问题的能力以及转化思想.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
经过直线l1:x-6y+4=0和直线l2:2x+y=5的交点,并且与直线l2垂直的直线方程是( )
| A、x-2y=0 |
| B、x+2y=0 |
| C、x+2y-4=0 |
| D、x-2y-4=0 |
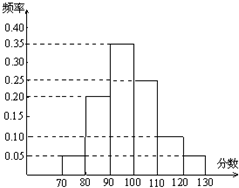 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.
已知ABCD为正方形,P是ABCD所成平面外一点,P在平面ABCD上的射影恰好是正方形的中心O.Q是CD的中点.