题目内容
12．某单位有男职工600名，女职工400人，在单位想了解本单位职工的运动状态，根据性别采取分层抽样的方法从全体职工中抽取100人，调查他们平均每天运动的时间（单位：小时），统计表明该单位职工平均每天运动的时间范围是[0，2]．若规定平均每天运动的时间不少于1小时的为“运动达人”，低于1小时的为“非运动达人”．根据调查的数据，按性别与是否为运动达人进行统计，得到如下2×2列联表．| 运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男 | 36 | ||
| 女 | 26 | ||
| 合计 | 100 |
（Ⅱ）将此样本的频率估计为总体的概率，随机调查该单位的3名男职工，设调查的3人中运动达人的人数为随机变量X，求X的分布列和数学期望E（X）及方差D（X）．
附表及公式：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 （I）计算K2，根据临界值表作出结论；
（II）分别计算X=0，1，2，3时的概率得出分布列，根据分布列得出数学期望和方差．
解答 解：（I）由题意，该单位根据性别采取分层抽样的方法抽取的100人中，有60人为男职工，40人为女职工，据此2×2列联表中的数据补充如下．
运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男 | 36 | 24 | 60 |
| 女 | 14 | 26 | 40 |
| 合计 | 50 | 50 | 100 |
由表中数据得观测值K2=$\frac{100×（36×26-14×24）^{2}}{60×40×50×50}$=6＞5.024，
所以在犯错误概率不超过0.025的前提下，可以认为性别与是否为运动达人有关．…（5分）
（2）随机调查一名男生，则这名男生为运动达人的概率为P=$\frac{36}{60}$=$\frac{3}{5}$．
X的可能取值为0，1，2，3．
∴P（X=0）=（1-$\frac{3}{5}$）3=$\frac{8}{125}$，P（X=1）=C31（$\frac{3}{5}$）（1-$\frac{3}{5}$）2=$\frac{36}{125}$，
P（X=2）=C32（$\frac{3}{5}$）2（1-$\frac{3}{5}$）=$\frac{54}{125}$，P（X=3）=（$\frac{3}{5}$）3=$\frac{27}{125}$．
∴X的分布列为：
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
点评 本题考查了独立性检验的应用，离散型随机变量的分布列、数学期望、方差的求法，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
2．已知数列{an}的通项公式为an=3n-50，则当n等于（ ）时，Sn取得最小值？
| A． | 16 | B． | 17 | C． | 18 | D． | 16或17 |
3．下列是x和y之间的一组数据
则y关于x的线性回归方程为y=bx+a，对应的直线必过点（ ）
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A． | （2，2） | B． | （$\frac{3}{2}，2$） | C． | （ $\frac{3}{2}，4$） | D． | （1，2） |
20．已知函数f（x）=$\sqrt{3}$sin（2x+$\frac{π}{3}$），其中x∈R，下列结论中正确的是（ ）
| A． | f（x）是最小正周期为π的偶函数 | |
| B． | f（x）的一条对称轴是 $x=\frac{π}{3}$ | |
| C． | f（x）的最大值为2 | |
| D． | 将函数$y=\sqrt{3}sin2x$的图象向左平移$\frac{π}{6}$个单位得到函数f（x）的图象 |
17．sin315°的值为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
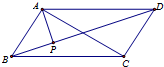如图，在平行四边形ABCD中，AP⊥BD，垂足为P，且AP=2，则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8．