题目内容
10.设复数z满足$\frac{{{{({1+i})}^2}}}{z}=1-i$,则z=( )| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
分析 利用复数的运算法则即可得出.
解答 解:复数z满足$\frac{{{{({1+i})}^2}}}{z}=1-i$,则z=$\frac{2i}{1-i}$=$\frac{2i(1+i)}{(1-i)(1+i)}$=i-1.
故选:C.
点评 本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\frac{5}{3}$,则其渐近线方程为( )
| A. | 2x±y=0 | B. | x±2y=0 | C. | 3x±4y=0 | D. | 4x±3y=0 |
2.已知向量$\overrightarrow{a}$=(5,k),$\overrightarrow{b}$=(2,-2),则使|$\overrightarrow{a}-\overrightarrow{b}$|≤5成立的充分不必要条件是( )
| A. | -6≤k≤2 | B. | -6≤k≤-2 | C. | -2≤k≤6 | D. | 2≤k≤6 |
20.在长为16cm的线段MN上任取一点P,以MP,NP为邻边作一矩形,则该矩形的面积大于60cm2的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
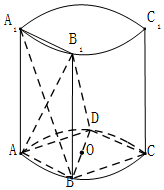 如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.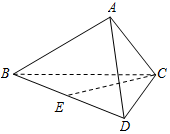 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.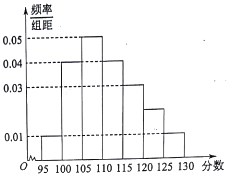 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.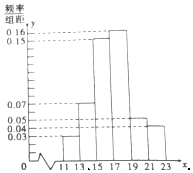 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.