题目内容
8.已知椭圆方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,其左焦点、上顶点和左顶点分别为F,A,B,坐标原点为O,且线段FO,OA,AB的长度成等差数列.(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点F的一条直线l交椭圆于点M,N,交y轴于点P,使得线段MN被点F,P三等分,求直线l的斜率.
分析 (Ⅰ)依题意有$c+\sqrt{{a^2}+{b^2}}=2b$,将其变形可得b=2c,结合椭圆的几何性质以及离心率公式可得$e=\frac{c}{a}=\frac{c}{{\sqrt{{b^2}+{c^2}}}}$,计算可得答案;
(Ⅱ)设直线l的方程为y=k(x+c),当k>0时,表示出k和xM、yM,将直线l的方程和椭圆方程联立,解可得xM、yM的值,由斜率公式计算可得k的值,同理分析k<0时可得k的值,综合可得答案.
解答 解:(Ⅰ)依题意有$c+\sqrt{{a^2}+{b^2}}=2b$,
把上式移项平方并把a2=b2+c2,代入得b=2c,
又由a2=b2+c2;
所以椭圆的离心率$e=\frac{c}{a}=\frac{c}{{\sqrt{{b^2}+{c^2}}}}=\frac{{\sqrt{5}}}{5}$.
(Ⅱ)设直线l的方程为y=k(x+c),
先研究k>0的情况,要使|MF|=|FP|,
则xM=-2c,${y_M}=-b•\sqrt{1-\frac{{{x_M}^2}}{a^2}}=-\frac{b}{{\sqrt{5}}}$,
因此$k=\frac{{0-(-\frac{b}{{\sqrt{5}}})}}{-c-(-2c)}=\frac{{2\sqrt{5}}}{5}$.
将直线l的方程和椭圆方程联立可得$\left\{\begin{array}{l}y=\frac{{2\sqrt{5}}}{5}(x+c)\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array}\right.$解得$\left\{\begin{array}{l}{x_M}=-2c\\{x_N}=c\end{array}\right.$
由于点N的横坐标为c,因此|PN|也等于|PF|,
同理,当k<0时,由对称性可知k=$-\frac{{2\sqrt{5}}}{5}$;
直线l的斜率为$\frac{{2\sqrt{5}}}{5}$或$-\frac{{2\sqrt{5}}}{5}$.
点评 本题考查椭圆的几何性质,涉及直线与椭圆的位置关系,关键是依据题意,求出椭圆的标准方程.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{5}$ | B. | 5 | C. | $2\sqrt{6}$ | D. | 25 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
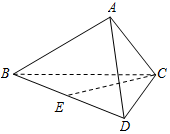 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.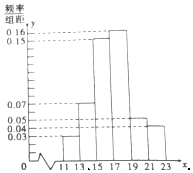 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.