题目内容
若（x2+
）5的二项展开式中x7项的系数为-10，则常数a= ．
| a |
| x |
考点：二项式定理
专题：计算题,二项式定理
分析：利用二项展开式的通项公式求得二项展开式中的第r+1项，令x的指数为7求得x7的系数，列出方程求解即可．
解答：
解：（x2+
）5的展开式的通项为Tr+1=C5rx10-2r（
）r=C5rx10-3rar
令10-3r=7得r=1，
∴x7的系数是aC51
∵x7的系数是-10，
∴aC51=-10，
解得a=-2．
故答案为：-2．
| a |
| x |
| a |
| x |
令10-3r=7得r=1，
∴x7的系数是aC51
∵x7的系数是-10，
∴aC51=-10，
解得a=-2．
故答案为：-2．
点评：本题主要考查了二项式系数的性质．二项展开式的通项公式是解决二项展开式的特定项问题的工具．
练习册系列答案
相关题目
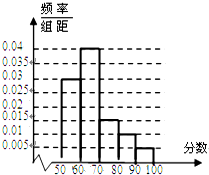在某中学举行的环保知识竞赛中，将三个年级参赛的学生的成绩进行整理后分为5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组，已知第二小组的频数是40，则成绩在80～100分的学生人数是（ ）| A、15 | B、18 | C、20 | D、25 |
函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=（
）x，则函数f（x）的反函数的零点为（ ）
| 1 |
| 3 |
| A、2 | B、-2 | C、3 | D、0 |
下列说法正确的是（ ）
| A、φ?{0} |
| B、0⊆Φ |
| C、0∈{（0，1）} |
| D、（1，2）∈{1，2，3} |
设函数f（x）=
，若f（a）=4，则实数a=（ ）
|
| A、-4或2 | B、-4或-2 |
| C、-2或4 | D、-2或2 |
使函数y=2sin（3x+φ）+2
cos（3x+φ）为奇函数，且在[0，
]上是减函数的一个φ值是（ ）
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|