题目内容
已知点Q(-
,1),边长为4的正方形内接于椭圆
+
=1(a>b>0),点F1、F2分别是椭圆的左右焦点.
(1)当椭圆的右准线为x=2
时,求椭圆的方程;
(2)当椭圆的离心率为多大时,双曲线
-
=1的焦距最小?并求出此最小焦距.
| 6 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)当椭圆的右准线为x=2
| 6 |
(2)当椭圆的离心率为多大时,双曲线
| x2 |
| a2 |
| y2 |
| 16b2 |
考点:椭圆的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:(1)由于边长为4的正方形内接于椭圆
+
=1(a>b>0),可得点(2,2)在椭圆上,
+
=1.
由椭圆的右准线为x=2
=
,及a2=b2+c2,联立解得即可.
(2)由(1)可知:
+
=1.可得
=
b2-1.椭圆的离心率e=
=
.
双曲线
-
=1的焦距=2
=2
=2
=4
,利用基本不等式的性质就看得出.
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| a2 |
| 4 |
| b2 |
由椭圆的右准线为x=2
| 6 |
| a2 |
| c |
(2)由(1)可知:
| 4 |
| a2 |
| 4 |
| b2 |
| b2 |
| a2 |
| 1 |
| 4 |
1-
|
2-
|
双曲线
| x2 |
| a2 |
| y2 |
| 16b2 |
| a2+16b2 |
b2(
|
b2(
|
4(b2-4+
|
解答:
解:(1)∵边长为4的正方形内接于椭圆
+
=1(a>b>0),
∴点(2,2)在椭圆上,∴
+
=1.
∵椭圆的右准线为x=2
=
,又a2=b2+c2,
联立解得c=
,a2=12,b2=6.或c=
,a2=16,b2=
.
∴椭圆的方程为
+
=1或
+
=1.
(2)由(1)可知:
+
=1.可得
=
b2-1.
e=
=
∵双曲线
-
=1的焦距=2
=2
=2
=4
≥4
=20,当且仅当b2=5取等号,双曲线的最小焦距为20.
椭圆的离心率e=
=
.
∴当椭圆的离心率为
时,双曲线
-
=1的焦距最小,最小焦距为20.
| x2 |
| a2 |
| y2 |
| b2 |
∴点(2,2)在椭圆上,∴
| 4 |
| a2 |
| 4 |
| b2 |
∵椭圆的右准线为x=2
| 6 |
| a2 |
| c |
联立解得c=
| 6 |
4
| ||
| 3 |
| 16 |
| 3 |
∴椭圆的方程为
| x2 |
| 12 |
| y2 |
| 6 |
| x2 |
| 16 |
| 3y2 |
| 16 |
(2)由(1)可知:
| 4 |
| a2 |
| 4 |
| b2 |
| b2 |
| a2 |
| 1 |
| 4 |
e=
1-
|
2-
|
∵双曲线
| x2 |
| a2 |
| y2 |
| 16b2 |
| a2+16b2 |
b2(
|
b2(
|
4(b2-4+
|
4×2
|
椭圆的离心率e=
2-
|
| ||
| 2 |
∴当椭圆的离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| 16b2 |
点评:本题考查椭圆方程的求法,椭圆性质的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
已知两条相交直线a、b,a∥平面α,则b与平面α的位置关系( )
| A、b∥α |
| B、b与α相交 |
| C、b?α |
| D、b∥α或b与α相交 |
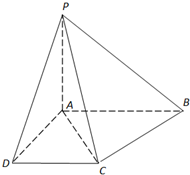 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.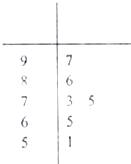 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.