题目内容
18.已知f(x)是定义在实数集R上的偶函数,且在(0,+∞)上递增,则( )| A. | f(20.7)<f(-log25)<f(-3) | B. | f(-3)<f(20.7)<f(-log25) | ||
| C. | f(-3)<f(-log25)<f(20.7) | D. | f(20.7)<f(-3)<f(-log25) |
分析 利用20.7<2<log25<3,f(x)在(0,+∞)上递增,可得f(20.7)<f(log25)<f(3),结合f(x)是定义在实数集R上的偶函数,即可得出结论.
解答 解:∵20.7<2<log25<3,f(x)在(0,+∞)上递增,
∴f(20.7)<f(log25)<f(3),
∵f(x)是定义在实数集R上的偶函数,
∴f(20.7)<f(-log25)<f(-3),
故选:A.
点评 本题考查函数的单调性与奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.已知等比数列{an}的前n项和为Sn,则下列一定成立的是( )
| A. | 若a4>0,则a2016<0 | B. | 若a5>0,则a2015<0 | ||
| C. | 若a4>0,则S2016>0 | D. | 若a5>0,则S2015>0 |
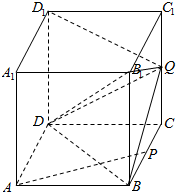 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.