题目内容
已知数列{an}的奇数项是首项为1的等差数列，偶数项是首项为2的等比数列，且满足a2+a3=a4，a11=a3+a4，记bn=a2n-1（n∈N*）
（1）求数列{bn}的通项公式；
（2）设数列{
}的前2014项和为T2014，求不超过T2014的最大整数．
（1）求数列{bn}的通项公式；
（2）设数列{
| bn2+bn+1 |
| bn2+bn |
考点：数列的求和,数列递推式
专题：等差数列与等比数列
分析：（1）根据等比数列和等差数列的通项公式，求出首项和公比，公差，即可求出相应的通项公式．
（2）求出数列{
}的通项公式，利用裂项法即可求前2014项和为T2014，即得到得到结论．
（2）求出数列{
| bn2+bn+1 |
| bn2+bn |
解答：
解：（1）设奇数项构成等差数列的公差为d，偶数项构成的等比数列的公比为q，
由a2+a3=a4，a11=a3+a4，得
，解得d=1，q=2，
则a2n-1=1+（n-1）×1=n，bn=a2n-1=n．
（2）
=
=1+
=1+
-
，
则数列{
}的前2014项和为T2014=（1+1-
）+（1+
-
）+…+（1+
-
）=2015-
，
则不超过T2014的最大整数为2014．
由a2+a3=a4，a11=a3+a4，得
|
则a2n-1=1+（n-1）×1=n，bn=a2n-1=n．
（2）
| bn2+bn+1 |
| bn2+bn |
| n2+n+1 |
| n2+n |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则数列{
| bn2+bn+1 |
| bn2+bn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
则不超过T2014的最大整数为2014．
点评：本题主要考查数列通项公式和前n项和的计算，利用裂项法法是解决本题的关键，考查学生的计算能力．
练习册系列答案
相关题目
等差数列前n项和为Sn，若a4+a7+a13=30，则S15的值是（ ）
| A、150 | B、65 | C、70 | D、75 |
已知全集U=R，集合A={y|y≥1}，B=（-∞，-1）∪（2，+∞），则A∪（∁UB）=（ ）
| A、[1，2] |
| B、[1，+∞） |
| C、[-1，+∞） |
| D、（-∞，-1]∪[1，+∞） |
如图所示，l1，l2是两条互相垂直的海岸线，C为一海岛，ABCD是一矩形渔场，为了扩大渔业规模，将该渔场改建成一个更大的矩形渔场AMPN，要求点D，N在海岸线l1上，点B，M在海岸线l2上，且两点M，N连线经过海岛C，已知AB=3km，AD=2km．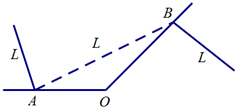
如图，某城市有一条公路从正西方AO通过市中心O后转向东北方OB，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，为了市民出行方便与城市环境问题，现要求市中心O到AB的距离为10km，设∠OAB=α．