题目内容
9.已知△ABC中,(a+b+c)(sinA+sinB-sinC)=asinB,其中A,B,C为△ABC的内角,a,b,c分别为A,B,C的对边,则C=( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
分析 使用正弦定理将角化边,整理出a,b,c的关系,代入余弦定理求出cosC.
解答 解:∵(a+b+c)(sinA+sinB-sinC)=asinB,∴(a+b+c)(a+b-c)=ab.
∴a2+b2-c2=-ab.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$.
∴C=$\frac{2π}{3}$.
故选:B.
点评 本题考查了正余弦定理的应用,属于基础题.

练习册系列答案
相关题目
19.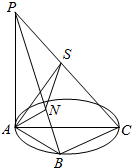 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
20.已知抛物线C:y2=2px(p>0),直线l与抛物线C交于A,B两点(不同于原点),以AB为直径的圆过坐标原点O,则关于直线l的判断正确的是( )
| A. | 过定点(4p,0) | B. | 过定点(2p,0) | C. | 过定点(p,0) | D. | 过抛物线焦点 |
4.已知实数a、b、c满足$\frac{\sqrt{5}b-c}{5a}$=$\frac{1}{4}$,那么关于b2与ac的大小关系的判断:①b2>ac,②b2=ac,③b2<ac,其中所有可能成立的是( )
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
14.图中阴影部分的面积用定积分表示为( )
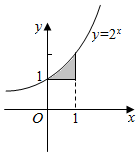
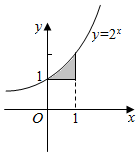
| A. | ${∫}_{0}^{1}$2xdx | B. | ${∫}_{0}^{1}$(2x-1)dx | C. | ${∫}_{0}^{1}$(2x+1)dx | D. | ${∫}_{0}^{1}$(1-2x)dx |