题目内容
设a＞0，f（x）=
+
是R上的偶函数．
（1）求a的值；
（2）判断并证明函数f（x）在[0，+∞）上的单调性；
（3）求函数的值域．
| 3x |
| a |
| a |
| 3x |
（1）求a的值；
（2）判断并证明函数f（x）在[0，+∞）上的单调性；
（3）求函数的值域．
考点：函数奇偶性的性质,函数的值域
专题：函数的性质及应用
分析：（1）利用偶函数的性质f（-x）=-f（x）得f（-1）=-f（1），代入函数解析式列出方程，可求得a的值；
（2）先判断出函数的单调性，再利用函数单调性的定义证明，即设值、作差、变形、定符号和下结论步骤；
（3）利用基本不等式求出f（x）的最小值，再得到函数的值域．
（2）先判断出函数的单调性，再利用函数单调性的定义证明，即设值、作差、变形、定符号和下结论步骤；
（3）利用基本不等式求出f（x）的最小值，再得到函数的值域．
解答：
解：（1）由题意得，f（x）=
+
是R上的偶函数，
所以f（-x）=f（x），则f（-1）=f（1），
即
+
=
+
，化简得a2=1，
又a＞0，所以a=1；
（2）由（1）得，f(x)=3x+
，则f（x）在[0，+∞）上是增函数，
任取x1、x2∈[0，+∞），且x1＜x2，
则f（x1）-f（x2）=3x1+
-（3x2+
）
=（3x1-3x2）+
=
，
由0≤x1＜x2，得3x1-3x2＜0，3x1•3x2＞1，
则f（x1）-f（x2）＜0，即f（x1）＜f（x2），
所以f（x）在（0，+∞）上是单调递增函数；
（3）因为3x＞0，所以f(x)=3x+
≥2
=2，
当且仅当3x=
时取等号，函数f（x）取到最小值2，
所以函数的值域是[2，+∞）．
| 3x |
| a |
| a |
| 3x |
所以f（-x）=f（x），则f（-1）=f（1），
即
| 3-1 |
| a |
| a |
| 3-1 |
| 3 |
| a |
| a |
| 3 |
又a＞0，所以a=1；
（2）由（1）得，f(x)=3x+
| 1 |
| 3x |
任取x1、x2∈[0，+∞），且x1＜x2，
则f（x1）-f（x2）=3x1+
| 1 |
| 3x1 |
| 1 |
| 3x2 |
=（3x1-3x2）+
| 3x2-3x1 |
| 3x1•3x2 |
| (3x1-3x2)(3x13x2-1) |
| 3x1•3x2 |
由0≤x1＜x2，得3x1-3x2＜0，3x1•3x2＞1，
则f（x1）-f（x2）＜0，即f（x1）＜f（x2），
所以f（x）在（0，+∞）上是单调递增函数；
（3）因为3x＞0，所以f(x)=3x+
| 1 |
| 3x |
3x•
|
当且仅当3x=
| 1 |
| 3x |
所以函数的值域是[2，+∞）．
点评：本题考查函数奇偶性的定义、性质，基本不等式求函数的最值，以及函数单调性的证明方法：定义法，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=loga（4-ax）在[-1，2]上单调递减，则正实数a的取值范围是（ ）
| A、a＞2 | ||
| B、1＜a＜2 | ||
C、
| ||
| D、以上都不对 |
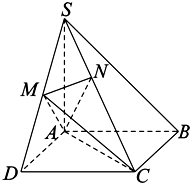如图，在四棱锥S-ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC，且交SC于点N．在空间直角坐标系O-xyz中，点B是点A（1，2，3）在坐标平面yOz内的射影，则|OB|等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|