题目内容
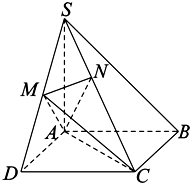 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.(Ⅰ)求证:SB∥平面ACM;
(Ⅱ)求证:平面SAC⊥平面AMN;
(Ⅲ)求二面角D-AC-M的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结BD交AC于E,连结ME,由△DSB的中位线定理,得ME∥SB,由此能证明SB∥平面ACM.
(Ⅱ)法一:由DC⊥SA,DC⊥DA,得DC⊥平面SAD,从而AM⊥DC,由等腰三角形性质得AM⊥SD,从而AM⊥平面SDC,进而SC⊥AM,由SC⊥AN,能证明平面SAC⊥平面AMN.
法二:以A为坐标原点,建立空间直角坐标系O-xyz,利用向量法能证明平面SAC⊥平面AMN.
(Ⅲ)法一:取AD中点F,则MF∥SA.作FQ⊥AC于Q,连结MQ,由已知得∠FQM为二面角D-AC-M的平面角,由此能求出二面角D-AC-M的余弦值.
法二:分别求出平面ABCD的一个法向量和平面ACM的一个法向量,由此利用向量法能求出二面角D-AC-M的余弦值.
(Ⅱ)法一:由DC⊥SA,DC⊥DA,得DC⊥平面SAD,从而AM⊥DC,由等腰三角形性质得AM⊥SD,从而AM⊥平面SDC,进而SC⊥AM,由SC⊥AN,能证明平面SAC⊥平面AMN.
法二:以A为坐标原点,建立空间直角坐标系O-xyz,利用向量法能证明平面SAC⊥平面AMN.
(Ⅲ)法一:取AD中点F,则MF∥SA.作FQ⊥AC于Q,连结MQ,由已知得∠FQM为二面角D-AC-M的平面角,由此能求出二面角D-AC-M的余弦值.
法二:分别求出平面ABCD的一个法向量和平面ACM的一个法向量,由此利用向量法能求出二面角D-AC-M的余弦值.
解答:
(选修2一1第109页例4改编)
(Ⅰ)证明:连结BD交AC于E,连结ME,
∵ABCD是正方形,∴E是BD的中点.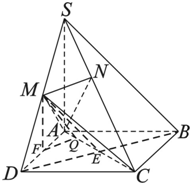
∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB.…(2分)
又ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.…(4分)
(Ⅱ)证法一:由条件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,且AM?平面SAD,∴AM⊥DC.
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC.SC?平面SDC,∴SC⊥AM.…(6分)
由已知SC⊥AN,∴SC⊥平面AMN.
又SC?平面SAC,∴平面SAC⊥平面AMN.…(8分)
(Ⅱ)证法二:如图,以A为坐标原点,建立空间直角坐标系O-xyz,
由SA=AB,可设AB=AD=AS=1,
则A(0,0,0),B(0,1,0),C(1,1,0),D(1,0,0),S(0,0,1),M(
,0,
).
∵
=(
,0,
),
=(-1,-1,1),
∴
•
=-
+
=0,∴
⊥
,即有SC⊥AM…(6分)
又SC⊥AN且AN∩AM=A.∴SC⊥平面AMN. 又SC?平面SAC,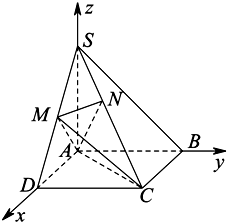
∴平面SAC⊥平面AMN.…(8分)
(Ⅲ)解法一:取AD中点F,则MF∥SA.
作FQ⊥AC于Q,连结MQ.
∵SA⊥底面ABCD,∴MF⊥底面ABCD.
∴FQ为MQ在平面ABCD内的射影.
∵FQ⊥AC,∴MQ⊥AC.
∴∠FQM为二面角D-AC-M的平面角. …(10分)
设SA=AB=a,在Rt△MFQ中,MF=
SA=
,FQ=
DE=
a,
∴tan∠FQM=
=
.
∴二面角D-AC-M的余弦值为
. …(12分)
(Ⅲ)解法二:∵SA⊥底面ABCD,
∴
是平面ABCD的一个法向量,
=(0,0,1).
设平面ACM的法向量为
=(x,y,z),
=(1,1,0),
=(
,0,
),
则
即
,∴
令x=-1,则
=( -1, 1,1).…(10分)
cos<
,
>=
=
=
,
由作图可知二面角D-AC-M为锐二面角
∴二面角D-AC-M的余弦值为
.…(12分)
(Ⅰ)证明:连结BD交AC于E,连结ME,
∵ABCD是正方形,∴E是BD的中点.

∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB.…(2分)
又ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.…(4分)
(Ⅱ)证法一:由条件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,且AM?平面SAD,∴AM⊥DC.
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC.SC?平面SDC,∴SC⊥AM.…(6分)
由已知SC⊥AN,∴SC⊥平面AMN.
又SC?平面SAC,∴平面SAC⊥平面AMN.…(8分)
(Ⅱ)证法二:如图,以A为坐标原点,建立空间直角坐标系O-xyz,
由SA=AB,可设AB=AD=AS=1,
则A(0,0,0),B(0,1,0),C(1,1,0),D(1,0,0),S(0,0,1),M(
| 1 |
| 2 |
| 1 |
| 2 |
∵
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| CS |
∴
| AM |
| CS |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| CS |
又SC⊥AN且AN∩AM=A.∴SC⊥平面AMN. 又SC?平面SAC,

∴平面SAC⊥平面AMN.…(8分)
(Ⅲ)解法一:取AD中点F,则MF∥SA.
作FQ⊥AC于Q,连结MQ.
∵SA⊥底面ABCD,∴MF⊥底面ABCD.
∴FQ为MQ在平面ABCD内的射影.
∵FQ⊥AC,∴MQ⊥AC.
∴∠FQM为二面角D-AC-M的平面角. …(10分)
设SA=AB=a,在Rt△MFQ中,MF=
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴tan∠FQM=
| ||||
|
| 2 |
∴二面角D-AC-M的余弦值为
| ||
| 3 |
(Ⅲ)解法二:∵SA⊥底面ABCD,
∴
| AS |
| AS |
设平面ACM的法向量为
| n |
| AC |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
则
|
|
|
令x=-1,则
| n |
cos<
| AS |
| n |
| ||||
|
|
| 1 | ||
1×
|
| ||
| 3 |
由作图可知二面角D-AC-M为锐二面角
∴二面角D-AC-M的余弦值为
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查二面角的余弦值的求法,涉及到线线、线面、面面平行与垂直的性质的应用,考查向量法的合理运用,考查空间思维能力的培养,是中档题.

练习册系列答案
相关题目
图中阴影部分表示的集合是( )


| A、∁U(A∩B) |
| B、∁U(A∪B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
如图中O′A′B′C′为四边形OABC的斜二测直观图,则原平面图形OABC是( )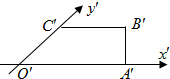
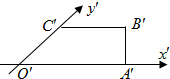
| A、直角梯形 |
| B、等腰梯形 |
| C、非直角且非等腰的梯形 |
| D、不可能是梯形 |
 设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间
设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间