题目内容
已知∠A=45°,∠B=75°,b=8,解这个三角形.
考点:解三角形
专题:计算题,解三角形
分析:由三角形的内角和定理,根据A和B的度数求出C的度数,由A,B的度数求出sinA,sinB的值,利用正弦定理求出a、c的值.
解答:
解:∵∠A=45°,∠B=75°,∴∠C=60°
∵b=8,
由正弦定理得a=
=
=8(
-1),
c=
=
=16
(
-1).
∵b=8,
由正弦定理得a=
| bsinA |
| sinB |
8•
| ||||||
|
| 3 |
c=
| bsinC |
| sinB |
8•
| ||||||
|
| 6 |
| 3 |
点评:本题属于解三角形的题型,涉及的知识有正弦定理,特殊角的三角函数值,两角和与差的正弦函数公式,根据正弦定理求出a是本题的突破点,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
若圆(x-5)2+(y-1)2=r2上有且仅有两点到直线4x+3y+2=0的距离等于1,则r的取值范围为( )
| A、[4,6] |
| B、(4,6) |
| C、[5,7] |
| D、(5,7) |
已知等比数列{an}中,a1+a6=33,a2a5=32,公比q>1,则a3+a8=( )
| A、66 | B、132 |
| C、64 | D、128 |
图中阴影部分表示的集合是( )


| A、∁U(A∩B) |
| B、∁U(A∪B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
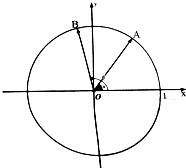 如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,
如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,