题目内容
11.若i是虚数单位,复数z满足(1-i)z=1,则|2z-3|=( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 设z=a+bi,得到(a+b)+(b-a)i=1,根据对应的系数相等得到a+b=1,a-b=0,求出a,b的值,求出复数的模即可.
解答 解:设z=a+bi,
则(1-i)z=(1-i)(a+bi)=1,
∴(a+b)+(b-a)i=1,
∴a+b=1,a-b=0,
∴a=b=$\frac{1}{2}$,
则|2z-3|=|2($\frac{1}{2}$+$\frac{1}{2}$i)-3|=|-2+i|=$\sqrt{5}$,
故选:B.
点评 本题考查了复数求模问题,熟练掌握复数的运算是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
3.某中学有3个社团,每位同学参加各个社团的可能性相同,甲、乙两位同学均参加其中一个社团,则这两位同学参加不同社团的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
1.如图,为一个半圆柱和一个半圆锥拼接而成的组合体的三视图,则该组合体的体积为( )
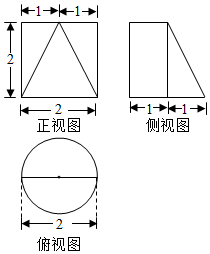

| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.