题目内容
3.某中学有3个社团,每位同学参加各个社团的可能性相同,甲、乙两位同学均参加其中一个社团,则这两位同学参加不同社团的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 由于每位同学参加各个社团的可能性相同,求出这两位同学同时参加同一个社团的概率,利用对立事件的概率即可求出结果.
解答 解:∵每位同学参加各个社团的可能性相同,
∴这两位同学同时参加一个社团的概率为:
P=3×$\frac{1}{3}$×$\frac{1}{3}$=$\frac{1}{3}$;
那么这两位同学参加不同社团的概率为
P′=1-P=1-$\frac{1}{3}$=$\frac{2}{3}$.
故选:C.
点评 本题考查了相互独立事件与等可能事件的概率计算问题,是基础题目.

练习册系列答案
相关题目
14.已知复数z满足$\frac{2z+m}{z-3}=i$,且z的实部与虚部之和为0,则实数m等于( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
11.若i是虚数单位,复数z满足(1-i)z=1,则|2z-3|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
8.若如图所示的程序框图输出的S是126,则条件①可以为( )
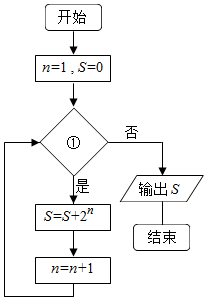

| A. | n≤5 | B. | n≤6 | C. | n≤7 | D. | n≤8 |