题目内容
平面内有四边形ABCD,
=2
,且AB=CD=DA,
=
,
=
,M是CD的中点.
(1)试用
,
表示
;
(2)若AB上有点P,PC和BM的交点为Q,已知PQ:QC=1:2,求AP:PB和BQ:QM.
| BC |
| AD |
| AD |
| a |
| BA |
| b |
(1)试用
| a |
| b |
| BM |
(2)若AB上有点P,PC和BM的交点为Q,已知PQ:QC=1:2,求AP:PB和BQ:QM.
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:(1)运用向量的中点表示,及向量的数乘,即可得到向量BM;
(2)设
=t
,
=λ
,运用向量的三角形法则,及平面向量的基本定理,得到λ,t的方程,解得即可.
(2)设
| BP |
| BA |
| BQ |
| BM |
解答:
解:(1)由于M是CD的中点,
则
=
(
+
)=
(
+
+2
)
=
+
,
(2)设
=t
,则
=
+
=
+
=
t
+
=
(
+t
)
设
=λ
=
+
,
由于
,
不共线,则有
,
解方程组,得λ=
,t=
.
故AP:PB=2:1,BQ:QM=4:5.
则
| BM |
| 1 |
| 2 |
| BC |
| BD |
| 1 |
| 2 |
| BA |
| AD |
| AD |
=
| 3 |
| 2 |
| a |
| 1 |
| 2 |
| b |
(2)设
| BP |
| BA |
| BQ |
| BC |
| CQ |
| BC |
| 2 |
| 3 |
| CP |
=
| 2 |
| 3 |
| BA |
| 2 |
| 3 |
| AD |
| 2 |
| 3 |
| a |
| b |
设
| BQ |
| BM |
| 3λ |
| 2 |
| a |
| λ |
| 2 |
| b |
由于
| BA |
| AD |
|
解方程组,得λ=
| 4 |
| 9 |
| 1 |
| 3 |
故AP:PB=2:1,BQ:QM=4:5.
点评:本题考查向量共线的定理和平面向量基本定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
不等式
<0成立的一个充分不必要条件是( )
| 1-x |
| x |
| A、x>1 | B、x<0或x>1 |
| C、0<x<1 | D、x≤0 |
将函数y=3sin(2x-
)的图象经过( )变换,可以得到函数y=3sin2x的图象.
| π |
| 4 |
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向右平移
| ||
D、沿x轴向左平移
|
下表中与数x对应的lgx值有且只有一个是错误的,则错误的是( )
| x | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| lgx | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
| A、lg6=1+a-b-c |
| B、lg8=3-3a-3c |
| C、lg12=3-b-2c |
| D、lg27=6a-3b |
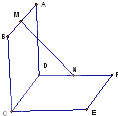 如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点.若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值.
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点.若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值.