题目内容
已知f(x)=2sin(
x+
),集合M={x||f(x)|=2,x>0},把M中的元素从小到大依次排成一列,得到数列{an}(n∈N*)
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b 1=1,bn+1=bn+a2n,求{bn}的通项公式.
| π |
| 3 |
| π |
| 6 |
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b 1=1,bn+1=bn+a2n,求{bn}的通项公式.
考点:数列与三角函数的综合
专题:综合题,等差数列与等比数列
分析:(1)由|f(x)|=2,可求得x,再由x>0可得集合M,从而可得a1,a2,a3,…,易判断其构成等差数列,从而得到数列{an}的通项公式;
(2)累加法:当n≥2时,bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,由bn+1-bn=a2n可求得bn,再检验n=1时是否适合该式即可;
(2)累加法:当n≥2时,bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,由bn+1-bn=a2n可求得bn,再检验n=1时是否适合该式即可;
解答:
解:(1)由|f(x)|=|2sin(
x+
)|=2,得sin(
x+
)=±1,
即
x+
=kπ+
,k∈Z,∴x=3k+1,k∈Z,
又x>0,所以M={x|x=3k+1,k∈N},
由题设a1=1,a2=4,a3=7,…,依次组成公差为3的等差数列,
所以数列{an}的通项公式an=3n-2,n∈N*;
(2)当n≥2时,
bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=a2n-1+a2n-2+…+a21+b1
=3(2n-1+2n-2+…+2)-2(n-1)+1
=3•
-2(n-1)+1
=3•2n-2n-3,
当n=1时,上式亦适合,
所求{bn}的通项公式为bn=3•2n-2n-3(n∈N*).
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
即
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
又x>0,所以M={x|x=3k+1,k∈N},
由题设a1=1,a2=4,a3=7,…,依次组成公差为3的等差数列,
所以数列{an}的通项公式an=3n-2,n∈N*;
(2)当n≥2时,
bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=a2n-1+a2n-2+…+a21+b1
=3(2n-1+2n-2+…+2)-2(n-1)+1
=3•
| 2(1-2n-1) |
| 1-2 |
=3•2n-2n-3,
当n=1时,上式亦适合,
所求{bn}的通项公式为bn=3•2n-2n-3(n∈N*).
点评:本题考查数列递推式、等差等比数列的通项公式及等比数列的前n项和公式,考查三角函数等有关知识,考查学生综合运用知识分析解决问题的能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
已知(x+1)5(2x-1)3=a8x8+a7x7+…+a1x+a0,则a7的值为( )
| A、-2 | B、28 | C、43 | D、52 |
在球O内任取一点P,则P点在球O的内接正四面体中的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设全集I=R,T={x|x2<x},M={x|x∉T},则M等于( )
| A、{x|x≥1} |
| B、{x|x>1} |
| C、{x|-1≤x≤0} |
| D、{x|x≥1或x≤0} |
已知A,B,C为圆O上三点,线段CO的延长线与线段AB有交点,若
=m
+n
,则m+n的范围是( )
| OC |
| OA |
| OB |
| A、(0,1) |
| B、(1,+∞) |
| C、(-1,0) |
| D、(-∞,-1) |
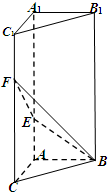 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,