题目内容
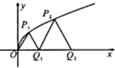 如图,抛物线y=
如图,抛物线y=| x |
考点:数列与解析几何的综合
专题:综合题,等差数列与等比数列
分析:求出P2(
,
),P3(3,
),|Q1Q2|=
,|Q2Q3|=
,可猜测|Qn-1Qn|=
,即xn-xn-1=
,利用叠加法,可得结论.
| 4 |
| 3 |
2
| ||
| 3 |
| 3 |
| 4 |
| 3 |
| 6 |
| 3 |
| 2n |
| 3 |
| 2n |
| 3 |
解答:
解:OP1的方程为y=
x,代入抛物线y=
可得P1(
,
),|OQ1|=
.
同理可得P2(
,
),P3(3,
),|Q1Q2|=
,|Q2Q3|=
,
可猜测|Qn-1Qn|=
,
∴xn-xn-1=
,
∴xn-x1=
+
+…+
,
∴xn=
(1+2+…+n)=
.
故答案为:xn=
.
| 3 |
| x |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
同理可得P2(
| 4 |
| 3 |
2
| ||
| 3 |
| 3 |
| 4 |
| 3 |
| 6 |
| 3 |
可猜测|Qn-1Qn|=
| 2n |
| 3 |
∴xn-xn-1=
| 2n |
| 3 |
∴xn-x1=
| 4 |
| 3 |
| 6 |
| 3 |
| 2n |
| 3 |
∴xn=
| 2 |
| 3 |
| n(n+1) |
| 3 |
故答案为:xn=
| n(n+1) |
| 3 |
点评:本题是抛物线与数列的综合,根据点在抛物线图象上,以及点之间的关系,找到坐标之间的关系,即数列的递推公式,再由递推公式求通项公式,属于综合题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
函数f(x)=2x2+2x-3的零点个数为( )
| A、0 | B、1 | C、2 | D、无数 |