题目内容
已知不等式|x+2|+|x|≤a的解集不是空集，则实数a的取值范围是 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：根据绝对值的意义|x+2|+|x|的最小值为2，再根据不等式|x+2|+|x|≤a的解集不是空集，可得a≥2．
解答：
解：|x+2|+|x|表示数轴上的x对应点到-2、0对应点的距离之和，它的最小值为2，
再根据不等式|x+2|+|x|≤a的解集不是空集，可得a≥2，
故答案为：{a|a≥2}．
再根据不等式|x+2|+|x|≤a的解集不是空集，可得a≥2，
故答案为：{a|a≥2}．
点评：本题主要考查绝对值的意义，绝对值不等式的解法，函数的能成立问题，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
方程log
x=2x-2014的实数根的个数为（ ）
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、不确定 |
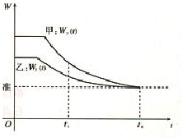国家环保总局对长期超标准排放污物，污染严重而又未进行治理的单位，规定出一定期限，强令在此期限内完成排污治理．如图是国家环保总局在规定的排污达标日期前，对甲、乙两家企业连续检测的结果（W表示排污量），哪个企业治理的效率比较高？为什么？若A={1，2，3}，B={1，2}，则A∩B=（ ）
| A、{1，2} | B、{3} |
| C、{1，2，3} | D、∅ |