题目内容

13．为迎接茶博会，要设计如图的一张矩形广告，该广告含有带下相等的左中右三个矩形栏目，这三栏的面积之比为60000cm2，四周空白的宽度为10cm，栏与栏之间的中缝空白的宽度为值5cm，怎样确定栏目的高与宽之比，能使整个矩形广告面积最小．

分析 根据矩形栏目面积确定高与宽的关系，从而可得整个矩形广告面积，再利用基本不等式，即可求得最值．

解答 解：设矩形栏目的高为acm，宽为bcm，则ab=20000，∴b=$\frac{20000}{a}$
广告的高为（a+20）cm，宽为（3b+30）cm（其中a＞0，b＞0）
广告的面积S=（a+20）（3b+30）=30（a+$\frac{40000}{a}$）+60600≥30×2$\sqrt{a×\frac{40000}{a}}$+60600=72600
当且仅当a=$\frac{40000}{a}$，即a=200时，取等号，此时b=100．
故当广告矩形栏目的高为200cm，宽为100cm时，可使广告的面积最小．

点评 本题考查函数模型的构建，考查基本不等式的运用，解题的关键是正确表示整个矩形广告面积，属于中档题．

练习册系列答案
相关题目
19．（1）化简：log89×log32-lg5-lg2+lne2
（2）化简：（-2${a}^{\frac{1}{3}}$${b}^{-\frac{3}{4}}$）•（-${a}^{\frac{1}{2}}$${b}^{-\frac{1}{3}}$）÷（-3${a}^{\frac{2}{3}}{b}^{-\frac{1}{4}}$）
4．下列命题中真命题是（2）（4）．
（1）若|$\overrightarrow{a}$|=1，则$\overrightarrow{a}$=±1；
（2）若$\overrightarrow{a}$≠$\overrightarrow{0}$，则$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$是单位向量；
（3）若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$；
（4）若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则$\overrightarrow{a}$、$\overrightarrow{b}$共线．
1．过抛物线y2=4x的焦点F的直线l交该抛物线于A，B两点，点A在第一象限，若|AF|=3，则直线l的斜率为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．$2\sqrt{2}$
8．等差数列{an}中，a2=1，a6=9，则{an}的前7项和S7=35．
18．已知$sinα=\frac{{\sqrt{5}}}{5}$且α是锐角，tanβ=-3，且β为钝角，则α+β的值为（　　）
A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{3π}{4}$
5．求函数f（x）=x3-3x2-9x+5的极值．
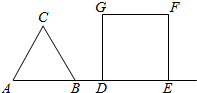2．如图所示，A、B、D、E四点在同一直线上，△ABC是边长为2的正三角形，DEFG是边长为2的正方形，在静止状态时，B点在D点的左侧，且$|{\overrightarrow{BD}}|=1$，让A点沿直线AB从左到右运动，当A点运动到E点时，运动结束．
（1）求在静止状态时，$\overrightarrow{BF}•\overrightarrow{CE}$的值；
（2）当A点运动时，求$\overrightarrow{BF}•\overrightarrow{CE}$的最小值．
3．抛物线y2=4x的焦点为F，过点F的直线交抛物线于A，B两点．
（1）若$\overrightarrow{AF}=2\overrightarrow{FB}$，求直线AB的斜率；
（2）求△OAB面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网