题目内容
已知在△ABC中，A=60°，a=
，b=
，求边长c和角B，C．
| 6 |
| 2 |
考点：正弦定理
专题：计算题,解三角形
分析：由正弦定理
=
可求得B=30°或150°，由a＞b进行判断取舍，再由勾股定理可求c．
| a |
| sinA |
| b |
| sinB |
解答：
解：由正弦定理
=
，得：
=
，
解得：sinB=
，
∴B=30°或150°，
因为a＞b，所以B=30°，
所以C=90°，c=
=2
，
综上B=30°，C=90°，c=2
．
| a |
| sinA |
| b |
| sinB |
| ||
| sin60° |
| ||
| sinB |
解得：sinB=
| 1 |
| 2 |
∴B=30°或150°，
因为a＞b，所以B=30°，
所以C=90°，c=
| a2+b2 |
| 2 |
综上B=30°，C=90°，c=2
| 2 |
点评：该题考查正弦定理及其应用，属基础题，利用正弦定理求出多解时要注意取舍的判断．
练习册系列答案
优学名师名题系列答案
相关题目
已知a、b∈R，“a＜b”是“2a＜3b”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
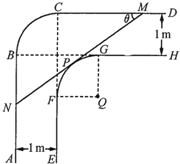一走廊拐角处的横截面如图所示，已知内壁FG和外壁BC都是半径为1m的四分之一圆弧，AB，DC分别与圆弧BC相切于B，C两点，EF∥AB，GH∥CD且两组平行墙壁间的走廊宽度都是1m．
在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩，并分成5组，得到频率分布直方图如图所示．已知成绩落在第2组[110，120）内的人数为8人．