题目内容
抛物线的顶点在原点,它的准线过双
-
=1(a>0,b>0)曲线的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为(
,
),求抛物线的方程和双曲线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 6 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:首先根据抛物线的准线过双曲线的焦点,可得p=2c,再利用抛物线与双曲线同过交点(
,
),求出c、p的值,进而结合双曲线的性质a2+b2=c2,求解即可
| 3 |
| 2 |
| 6 |
解答:
解:由题设知,抛物线以双曲线的右焦点为焦点,准线过双曲线的左焦点,∴p=2c.
设抛物线方程为y2=4c•x,
∵抛物线过点(
,
),∴6=4c•
.
∴c=1,故抛物线方程为y2=4x.
又双曲线
-
=1过点(
,
),
∴
-
=1.
又a2+b2=c2=1,∴
-
=1.
∴a2=
或a2=9(舍).
∴b2=
,
故双曲线方程为:4x2-
=1.
设抛物线方程为y2=4c•x,
∵抛物线过点(
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
∴c=1,故抛物线方程为y2=4x.
又双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 6 |
∴
| 9 |
| 4a2 |
| 6 |
| b2 |
又a2+b2=c2=1,∴
| 9 |
| 4a2 |
| 6 |
| 1-a2 |
∴a2=
| 1 |
| 4 |
∴b2=
| 3 |
| 4 |
故双曲线方程为:4x2-
| y2 | ||
|
点评:本题考查了抛物线和双曲线方程的求法:待定系数法,熟练掌握圆锥曲线的性质是解题的关键,同时考查了学生的基本运算能力与运算技巧.

练习册系列答案
相关题目
已知f(x)为R上的增函数,且f(log2x)>f(1),则x的取值范围为( )
| A、(2,+∞) | ||
B、(0,
| ||
C、(
| ||
| D、(0,1)∪(2,+∞) |
 如图,直四棱柱ABCD-A1B1C11中,AB∥CD,AD⊥AB,AB=2,AD=
如图,直四棱柱ABCD-A1B1C11中,AB∥CD,AD⊥AB,AB=2,AD=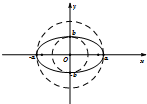 圆锥曲线中不同曲线的性质都是有一定联系的,比如圆可以看成特殊的椭圆,所以很多圆的性质结论可以类比到椭圆,例如;如图所示,椭圆C:
圆锥曲线中不同曲线的性质都是有一定联系的,比如圆可以看成特殊的椭圆,所以很多圆的性质结论可以类比到椭圆,例如;如图所示,椭圆C: