题目内容

11．祖暅原理：“幂势既同，则积不容异”．它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面积恒相等，则体积相等．设A，B为两个同高的几何体，p：A，B的体积不相等，q：A，B在等高处的截面积不恒相等，根据祖暅原理可知，q是p的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据逆否命题的等价性判断￢p是￢q的关系即可．

解答 解：￢q：A，B在等高处的截面积恒相等，￢p：A，B的体积相等，
则由祖暅原理可知，￢p是￢q的必要不充分条件，
则q是p的必要不充分条件，
故选：B

点评 本题主要考查充分条件和必要条件的条件的判断，根据逆否命题的等价性进行转化是解决本题的关键．

练习册系列答案
相关题目
1．O是平面上一定点，△ABC中AB=AC，一动点P满足：$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\overrightarrow{AB}$+$\overrightarrow{AC}$），λ∈（0，+∞），则直线AP通过△ABC的①②③④（请在横线上填入正确的编号）
①外心    ②内心    ③重心    ④垂心．
2．己知（2x-$\frac{1}{\sqrt{x}}$）5
（Ⅰ）求展开式中含$\frac{1}{x}$项的系数
（Ⅱ）设（2x-$\frac{1}{\sqrt{x}}$）5的展开式中前三项的二项式系数之和为M，（1+ax）6的展开式中各项系数之和为N，若4M=N，求实数a的值．
19．已知f（x）是R上的奇函数，当x≥0时，f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（x+1），0≤x＜1}\\{|x-3|，x≥1}\end{array}\right.$，则函数y=f（x）-$\frac{1}{2}$的所有零点之和是（　　）
A．5+$\sqrt{2}$B．1-$\sqrt{2}$C．$\sqrt{2}$-1D．5-$\sqrt{2}$
6．若（$\frac{x}{2}$-$\frac{2}{x}$）n的展开式中前三项的二项式系数之和等于22，
（1）求该展开式中含$\frac{1}{{x}^{2}}$项的系数
（2）求展开式中系数绝对值最大的项的系数．
16．在如图的程序框图中，若输入的x值为2，则输出的y值为（　　）
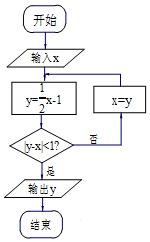
A．0B．$\frac{1}{2}$C．-$\frac{3}{2}$D．-1
3．在极坐标系中，点M（1，$\frac{π}{2}$），曲线C的方程为ρsin2θ=cosθ．以极点O为原点，以极轴为x轴正半轴建立直角坐标系．
（Ⅰ）求点M的直角坐标及曲线C的直角坐标方程；
（Ⅱ）斜率为-1的直线l过点M，且与曲线C交于A，B两点，求点M到A，B两点的距离之积．
10．求点M（1，-1，2）到直线L：$\left\{\begin{array}{l}{x-y-z+1=0}\\{2x-y+z-2=0}\end{array}\right.$ 的距离．
11．△ABC的内角A、B、C的对边分别为a、b、c．已知a=$\sqrt{5}$，b=3，cosA=$\frac{2}{3}$，则c=（　　）
A．3B．$\sqrt{3}$C．2D．$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网