题目内容
如果二次函数y=5x2+mx+4在区间（-∞，-1]上是减函数，则m的取值范围是（ ）
| A、（-∞，-10] |
| B、（-∞，10] |
| C、[10，+∞） |
| D、[-10，+∞） |
考点：二次函数的性质
专题：函数的性质及应用
分析：首先求出函数的顶点式，进一步确定对称轴的方程，根据对称轴方程与固定区间的关系确定结果．
解答：
解：函数y=5x2+mx+4=5（x+
）2+6-
，
则对称轴方程：x=-
，
函数在区间（-∞，-1]上为减函数
则：-
≥-1
解得：m≤10．
故选：B．
| m |
| 10 |
| m2 |
| 20 |
则对称轴方程：x=-
| m |
| 10 |
函数在区间（-∞，-1]上为减函数
则：-
| m |
| 10 |
解得：m≤10．
故选：B．
点评：本题考查的知识要点：二次函数的顶点式与一般式的互化，对称轴和单调区间的关系．
练习册系列答案
相关题目
已知函数f（x）=
，则f（-10）的值是（ ）
|
| A、-2 | B、-1 | C、0 | D、1 |
如图是某三棱锥的三视图，则这个三棱锥的体积是（ ）
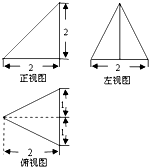
A、
| ||
B、
| ||
C、
| ||
D、
|
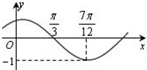函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）的图象如图所示，为了得到g（x）=Acosωx的图象，可以将f（x）的图象（ ）A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|