题目内容
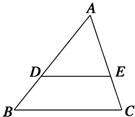如图所示，D、E分别是△ABC的边AB、AC上的点，DE∥BC，且| AD |
| DB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平行线分线段成比例定理
专题：选作题,立体几何
分析：根据已知可得到△ADE∽△ABC，可得到其相似比与面积比，从而不难求得△ADE与四边形DBCE的面积的比．
解答：
解：∵
=2，∴
=
又∵DE∥BC
∴△ADE∽△ABC，相似比是2：3，面积的比是4：9
设△ADE的面积是4a，则△ABC的面积是9a，四边形DBCE的面积是5a
∴△ADE与四边形DBCE的面积的比是
．
故选：C．
| AD |
| DB |
| AD |
| AB |
| 2 |
| 3 |
又∵DE∥BC
∴△ADE∽△ABC，相似比是2：3，面积的比是4：9
设△ADE的面积是4a，则△ABC的面积是9a，四边形DBCE的面积是5a
∴△ADE与四边形DBCE的面积的比是
| 4 |
| 5 |
故选：C．
点评：本题主要考查了相似三角形的判定与性质的理解及运用．
练习册系列答案
相关题目
设双曲线
-
=1（a＞0，b＞0）的离心率e=2，右焦点F（c，0），方程ax2+bx-c=0的两个根分别为x1，x2，则点P（x1，x2）在（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、圆x2+y2=10内 |
| B、圆x2+y2=10上 |
| C、圆x2+y2=10外 |
| D、以上三种情况都有可能 |
函数y=sin2x-sinx+2的最大值是（ ）
| A、2 | B、3 | C、4 | D、5 |
函数f（x）=
+mx在[1，2]上是增函数，则m的取值范围为（ ）
| 1 |
| x |
A、[
| ||
| B、[1，4] | ||
| C、[1，+∞） | ||
| D、（-∞，-1] |
