题目内容
已知函数f(x)=
,若存在实数m∈[-1,1],使得f(m)=1,则实数k的取值范围是 .
| x-k+2 |
| x2+1 |
考点:函数的值域
专题:函数的性质及应用
分析:原命题等价于k=-m2+m+1在m∈[-1,1]的值域,由二次函数的区间最值可得.
解答:
解:由题意可得存在实数m∈[-1,1],使得f(m)=
=1,
变形可得k=-m2+m+1=-(m-
)2+
,
可看作关于m的二次函数,开口向下,
故当m∈[-1,
]时,关于m的函数单调递增,
当m∈[
,1]时,关于m的函数单调递减,
由对称性可知当m=
时,k取最大值
,
当m=-1时,k取最小值-1,
故实数k的取值范围为[-1,
]
故答案为:[-1,
]
| m-k+2 |
| m2+1 |
变形可得k=-m2+m+1=-(m-
| 1 |
| 2 |
| 5 |
| 4 |
可看作关于m的二次函数,开口向下,
故当m∈[-1,
| 1 |
| 2 |
当m∈[
| 1 |
| 2 |
由对称性可知当m=
| 1 |
| 2 |
| 5 |
| 4 |
当m=-1时,k取最小值-1,
故实数k的取值范围为[-1,
| 5 |
| 4 |
故答案为:[-1,
| 5 |
| 4 |
点评:本题考查二次函数的区间最值,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
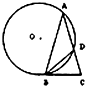 如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC=
如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC=