题目内容
15．社区主任要为小红等4名志愿者和他们帮助的2位老人拍照，要求排成一排，小红必须与两位老人都相邻，且两位老人不能排在两端，则不同的排法种数为（ ）| A． | 24 | B． | 20 | C． | 16 | D． | 12 |
分析 小红必须与两位老人都相邻，用捆绑法，有A22=2，两位老人不排在两端，则小红与2位老人在2、3、4或3、4、5位置，其余有A33=6，利用乘法原理即可得出结论．
解答 解：小红必须与两位老人都相邻，用捆绑法，有A22=2，两位老人不排在两端，则小红与2位老人在2、3、4或3、4、5位置，其余有A33=6，
故共有2×2×6=24种，
故选：A．
点评 本题考查排列、组合的实际应用，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
5．已知z=$\frac{（1-i）^{2}}{1+i}$，则z的共轭复数的虚部为（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
3．已知函数$f（x）=\frac{1}{3}{x^3}-{x^2}+ax-5$在[-1，2]上不单调，则实数a的取值范围是（ ）
| A． | [-3，1） | B． | （-3，0） | C． | （-3，1） | D． | （-3，1] |
7．已知数列{an}满足a1=60，an+1-an=2n，则$\frac{{a}_{n}}{n}$的最小值为（ ）
| A． | $\frac{29}{2}$ | B． | 2$\sqrt{60}$ | C． | $\frac{29}{4}$ | D． | $\frac{102}{7}$ |
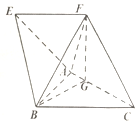如图，在四棱锥A-BCFE中，四边形EFCB为梯形，EF∥BC，且EF=$\frac{3}{4}$BC，△ABC是边长为2的正三角形，顶点F在AC上的射影为点G，且FG=$\sqrt{3}$，CF=$\frac{{\sqrt{21}}}{2}$，BF=$\frac{5}{2}$．