题目内容
9.已知函数f(x)=x2+4ax+2在区间(-∞,6)上是减函数,则实数a的取值范围是(-∞,-3].分析 函数f(x)=x2+4ax+2的对称轴方程为x=-2a,图象是开口向上的抛物线,由此根据函数f(x)=x2+4ax+2在区间(-∞,6)上是减函数,能求出实数a的取值范围.
解答 解:∵函数f(x)=x2+4ax+2在区间(-∞,6)上是减函数,
函数f(x)=x2+4ax+2的对称轴方程为x=-2a,图象是开口向上的抛物线,
∴-2a≥6,解得a≤-3.
∴实数a的取值范围是(-∞,-3].
故答案为:(-∞,-3].
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意二次函数的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设P是△ABC内一点,且$\overrightarrow{AP}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$,$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$+$\overrightarrow{AP}$=( )
| A. | $\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\frac{4}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AC}$ |
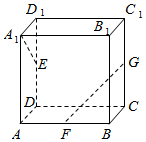 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,F为PC的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,F为PC的中点,PA=2AB=2.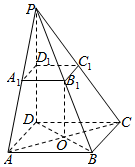 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.