题目内容
7.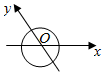 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
分析 $\overrightarrow{OP}$=3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,计算${\overrightarrow{OP}}^{2}$开方即为|$\overrightarrow{OP}$|.
解答 解:${\overrightarrow e_1}$•${\overrightarrow e_2}$=cos120°=-$\frac{1}{2}$.
∴|$\overrightarrow{OP}$|2=(3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$)2=9${\overrightarrow{{e}_{1}}}^{2}$+12$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$+4${\overrightarrow{{e}_{2}}}^{2}$=9-6+4=7.
∴|$\overrightarrow{OP}$|=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查了平面向量的数量级运算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设P是△ABC内一点,且$\overrightarrow{AP}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$,$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$+$\overrightarrow{AP}$=( )
| A. | $\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\frac{4}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AC}$ |
17.下列四个命题,其中是真命题的是( )
| A. | “两个全等三角形的周长相等”的逆命题 | |
| B. | “若一个整数的末位数字是0,则这个整数能被2整除”的否命题 | |
| C. | “对顶角相等”的逆否命题 | |
| D. | ?x0∈R,x02-x0+1<0 |
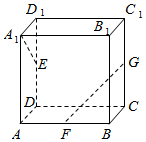 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.