题目内容
6．计算：$\sqrt{2}-1≈0.414，\sqrt{3}-\sqrt{2}$≈0.318；∴$\sqrt{2}-1＞\sqrt{3}-\sqrt{2}$；又计算：$\sqrt{5}-2≈0.236，\sqrt{6}-\sqrt{5}≈0.213，\sqrt{7}-\sqrt{6}$≈0.196，∴$\sqrt{5}-2＞\sqrt{6}-\sqrt{5}$，$\sqrt{6}-\sqrt{5}＞\sqrt{7}-\sqrt{6}$．（1）分析以上结论，试写出一个一般性的命题．
（2）判断该命题的真假，并给出证明．
分析 （1）根据所给结论，可写出一个一般性的命题．
（2）利用综合法证明命题是真命题．
解答 解：（1）一般性的命题n是正整数，则$\sqrt{n+1}$-$\sqrt{n}$＞$\sqrt{n+2}$-$\sqrt{n+1}$．
（2）命题是真命题．
∵$\sqrt{n+1}$-$\sqrt{n}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$，$\sqrt{n+2}$-$\sqrt{n+1}$=$\frac{1}{\sqrt{n+2}+\sqrt{n+1}}$，$\frac{1}{\sqrt{n+1}+\sqrt{n}}$＞$\frac{1}{\sqrt{n+2}+\sqrt{n+1}}$，
∴$\sqrt{n+1}$-$\sqrt{n}$＞$\sqrt{n+2}$-$\sqrt{n+1}$．
点评 本题考查归纳推理，考查综合法的运用，属于基础题．
练习册系列答案
相关题目
6．
某公司为确定2017年度投入某种产品的宣传费，需了解年宣传费x（单位：万元）对年销售收益y（单位：万元）的影响，2016年在若干地区各投入4万元的宣传费，并将各地的销售收益的数据作了初步处理，得到下面的频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度，并估计对应销售收益的平均值（以各组的区间中点值代表该组的取值）；
（Ⅱ）该公司按照类似的研究方法，测得一组数据如表所示：
表中的数据显示，y与x之间存在线性相关关系，求y关于x的回归直线方程；
（Ⅲ）由（Ⅱ）知，当宣传费投入为10万元时，销售收益大约为多少万元？
附：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
某公司为确定2017年度投入某种产品的宣传费，需了解年宣传费x（单位：万元）对年销售收益y（单位：万元）的影响，2016年在若干地区各投入4万元的宣传费，并将各地的销售收益的数据作了初步处理，得到下面的频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度，并估计对应销售收益的平均值（以各组的区间中点值代表该组的取值）；
（Ⅱ）该公司按照类似的研究方法，测得一组数据如表所示：
| 宣传费x（单位：万元） | 3 | 2 | 1 | 5 | 4 |
| 销售收益y（单位：万元） | 2 | 3 | 2 | 7 | 5 |
（Ⅲ）由（Ⅱ）知，当宣传费投入为10万元时，销售收益大约为多少万元？
附：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
7．若将函数$y=2sin（{2x+\frac{π}{6}}）$的图象向左平移$\frac{π}{12}$个单位长度，则平移后图象的对称轴方程为（ ）
| A． | $x=\frac{kπ}{2}+\frac{π}{12}（{k∈Z}）$ | B． | $x=\frac{kπ}{2}+\frac{π}{8}（{k∈Z}）$ | C． | $x=kπ+\frac{π}{12}（{k∈Z}）$ | D． | $x=kπ+\frac{π}{8}（{k∈Z}）$ |
1．点M的直角坐标（2$\sqrt{3}$，-2）化成极坐标为（ ）
| A． | （4，$\frac{5π}{6}$） | B． | （4，$\frac{2π}{3}$） | C． | （4，$\frac{5π}{3}$） | D． | （4，$\frac{11π}{6}$） |
15．函数$f（x）=2sin（ωx+ϕ）（ω＞0，-\frac{π}{2}＜ϕ＜\frac{π}{2}）$的部分图象如图所示，则ω，ϕ的值为（ ）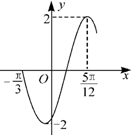
| A． | $2\;，\;\frac{2π}{3}$ | B． | $2\;，\;-\frac{π}{3}$ | C． | $1\;，\;\frac{π}{12}$ | D． | $1\;，\;-\frac{π}{12}$ |