题目内容
4.已知曲线C1的参数方程为:$\left\{\begin{array}{l}{x=cosθ}\\{y=1+sinθ}\end{array}$(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为:ρ=4sin(θ+$\frac{π}{3}$),直线l的极坐标方程为θ=$\frac{π}{6}$.(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若曲线C1和曲线C2与直线l分别交于非坐标原点的A,B两点,求|AB|的值.
分析 (1)利用三种方程的转化方法,求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)利用极径的意义,求|AB|的值.
解答 解:(1)曲线C1的参数方程为:$\left\{\begin{array}{l}{x=cosθ}\\{y=1+sinθ}\end{array}$(θ为参数),
普通方程为x2+(y-1)2=1,
曲线C2的极坐标方程为:ρ=4sin(θ+$\frac{π}{3}$),即ρ=2sinθ+2$\sqrt{3}$cosθ,
直角坐标方程为x2+y2=2y+2$\sqrt{3}$x;
(2)曲线C1的极坐标方程为:ρ=2sinθ
将θ=$\frac{π}{6}$代入C1的极坐标方程得ρ1=2,
将θ=$\frac{π}{6}$代入C2的极坐标方程得ρ2=4,
∴|AB|=ρ2-ρ1=3.--------------------------(10分)
点评 本题考查三种方程的转化方法,考查极径的意义,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
14.已知O为正△ABC内的一点,且满足$\overrightarrow{OA}+λ\overrightarrow{OB}+(1+λ)\overrightarrow{OC}=\overrightarrow 0$,若△OAB的面积与△OBC的面积的比值为3,则λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
15.已知集合$A=\{x|x<2\},B=\{x|\frac{x}{x-1}<1\},R$为实数集,则集合A∩(∁RB)=( )
| A. | R | B. | (-∞,2) | C. | (1,2) | D. | [1,2) |
12.已知函数f(x)=lnx-x2与g(x)=(x-2)2-$\frac{1}{2x-4}$-m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
| A. | (-∞,1-ln2) | B. | (-∞,1-ln2] | C. | (1-ln2,+∞) | D. | [1-ln2,+∞) |
4.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )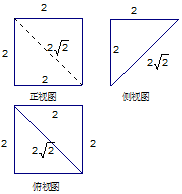

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.