题目内容
16.若平面向量$\overrightarrow a=(-1,2)$,$|{\overrightarrow b}|=3\sqrt{5}$,设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,且cosθ=-1,则$\overrightarrow b$的坐标为(3,-6).分析 利用两个向量共线的性质可得$\overrightarrow a$与$\overrightarrow b$的夹角π,设$\overrightarrow{b}$=-λ•$\overrightarrow{a}$,λ>0,根据$|{\overrightarrow b}|=3\sqrt{5}$,求得λ的值,可得$\overrightarrow b$的坐标.
解答 解:∵平面向量$\overrightarrow a=(-1,2)$,$|{\overrightarrow b}|=3\sqrt{5}$,设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,且cosθ=-1,
∴$\overrightarrow a$与$\overrightarrow b$的夹角θ=π,设$\overrightarrow{b}$=-λ•$\overrightarrow{a}$=(λ,-2λ),λ>0,
∴λ2+(-2λ)2=${(3\sqrt{5})}^{2}$,∴λ=3,∴$\overrightarrow b$的坐标为(3,-6),
故答案为:(3,-6).
点评 本题主要考查两个向量共线的性质,求向量的模,属于基础题.

练习册系列答案
相关题目
4.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )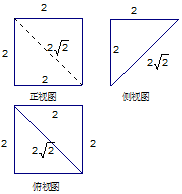

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
1.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,若在曲线C的右支上存在点P,使得△PF1F2的内切圆半径为a,圆心记为M,又△PF1F2的重心为G,满足MG∥F1F2,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
8.已知抛物线x2=4y的焦点为F,准线为l,抛物线的对称轴与准线交于点Q,P为抛物线上的动点,|PF|=m|PQ|,当m最小时,点P恰好在以F,Q为焦点的椭圆上,则椭圆的离心率为( )
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
5.若关于x的方程x2-xlnx+2=k(x+2)在[$\frac{1}{2}$,+∞)上有两解,则实数k的取值范围为( )
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
6.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |