题目内容
17.函数y=sin(2x-$\frac{π}{6}$)的单调增区间是[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z).分析 由条件利用正弦函数的单调性,得出结论.
解答 解:对于函数y=sin(2x-$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
求得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,可得它的增区间为[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z),
故答案为:[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z).
点评 本题主要考查正弦函数的单调性,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10.设复数z=1+i(i是虚数单位),则$\frac{4}{z}$+z=( )
| A. | 1+3i | B. | 1-3i | C. | 3+3i | D. | 3-i |
8.已知命题p:?x>0,总有2x>1,则¬p为( )
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | ||
| C. | $?{x_0}≤0,使得{2^{x_0}}≤1$ | D. | $?{x_0}>0,使得{2^{x_0}}≤1$ |
6.设f′(x)是f(x)=$\frac{1-x}{1+x}$的导数,则$\frac{f′(3)}{f(3)}$=( )
| A. | $\frac{1}{4}$ | B. | 0 | C. | -$\frac{3}{4}$ | D. | 1 |
7.集合P={3,4,5},Q={6,7},M={(a,b)|a∈P,b∈Q},则M的子集个数为( )
| A. | 6 | B. | 12 | C. | 32 | D. | 64 |
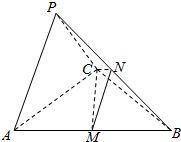 如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.
如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.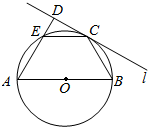 如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.
如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.