题目内容
已知sinα=
,sin(α+β)=
,α∈(0,
),α+β∈(
,π),求β的值.
| 4 |
| 7 |
| 3 |
| 5 |
| 14 |
| 3 |
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先根据已知条件求得cosα和cos(α+β)的值,进而根据两角和公式利用cosβ=cos(α+β-α)求得答案.
解答:
解:由已知得cosα=
,cos(α+β)=-
,
由cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=
,
又α∈(0,
),α+β∈(
,π),
∴β=
.
| 1 |
| 7 |
| 11 |
| 14 |
由cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=
| 1 |
| 2 |
又α∈(0,
| π |
| 2 |
| π |
| 2 |
∴β=
| π |
| 3 |
点评:本题主要考查了两角和与差的正弦公式的应用.解题的关键时找到cosβ=cos(α+β-α).

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
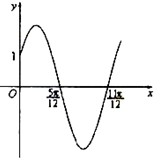 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<ω<
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<ω<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(2x-
| ||
D、f(x)=2sin(2x-
|
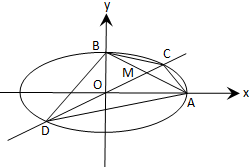 如图所示,已知A,B分别是椭圆E:
如图所示,已知A,B分别是椭圆E: