题目内容
已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则
•
的值为 .
| AE |
| AF |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的三角形法则、数量积运算即可得出.
解答:
解:如图所示,
∵
=
(
+
),
=
.
∴
•
=
(
+
)•
=
•
+
•
=
a2cos60°×2
=
a2.
故答案为:
a2.

∵
| AE |
| 1 |
| 2 |
| AB |
| AC |
| AF |
| 1 |
| 2 |
| AD |
∴
| AE |
| AF |
| 1 |
| 4 |
| AB |
| AC |
| AD |
=
| 1 |
| 4 |
| AB |
| AD |
| 1 |
| 4 |
| AC |
| AD |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了向量的三角形法则、数量积运算,属于基础题.

练习册系列答案
相关题目
下列运算结果正确的是( )
A、
| ||||||
| B、log36-log33=1 | ||||||
C、
| ||||||
D、log2
|
图中的图象所表示的函数的解析式为( )
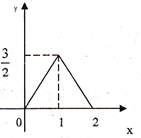

A、y=
| ||
B、y=
| ||
C、y=
| ||
| D、2-|x-1|(0≤x≤2) |
已知函数f(x)=ax-2+3(a>0且a≠1)恒过定点P,则点P的坐标为( )
| A、(0,3) |
| B、(0,4) |
| C、(2,4) |
| D、(3,4) |