题目内容
袋子里有2颗白球,3颗黑球,由甲、乙两人依次各抽取一个球,抽取后不放回,若每颗球被抽到的机会均等,则甲、乙两人所得之球颜色互异的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:先计算甲、乙两人依次各抽取一个球,抽取后不放回的情况种数,再计算甲、乙两人所得之球颜色互异的情况种数,进而代入古典概型概率计算公式,可得答案.
解答:
解:∵袋子里有2颗白球,3颗黑球,共5颗,
故甲、乙两人人依次各抽取一个球,抽取后不放回共有
=10种不同情况;
其中甲、乙两人人所得之球颜色互异的情况有:
•
=6种,
故甲、乙两人三人所得之球颜色互异的概率P=
=
,
故答案为:
故甲、乙两人人依次各抽取一个球,抽取后不放回共有
| C | 2 5 |
其中甲、乙两人人所得之球颜色互异的情况有:
| C | 1 2 |
| C | 1 3 |
故甲、乙两人三人所得之球颜色互异的概率P=
| 6 |
| 10 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:此题考查了古典概型概率计算公式,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的上底面面积是
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的上底面面积是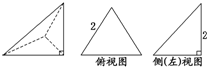 已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为
已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为