题目内容
在直角坐标系xoy中，已知向量
=（-1，2），点A（8，0），B（ksinθ，t），（0≤θ≤
，t∈R）
（1）若
⊥
，且|
|=|
|，求向量
．
（2）若向量
与向量
共线，当k＞4，且tsinθ取得最大值为4时，求
•
．
| a |
| π |
| 2 |
（1）若
| AB |
| a |
| OA |
| AB |
| OB |
（2）若向量
| AB |
| a |
| OA |
| OB |
考点：平面向量数量积的运算,数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：（1）根据已知，写出
=(ksinθ-8，t)，然后，根据垂直条件，求解即可；
（2）设
=λ
，然后，借助于向量运算，构造关系式，tsinθ=（16-2ksinθ）sinθ，然后，进行求解．
| AB |
（2）设
| AB |
| a |
解答：
解：（1）∵点A（8，0），B（ksinθ，t），
∴
=(ksinθ-8，t)，
∵
⊥
，
∴-ksinθ+8+2t=0，①
∵|
|=|
|，
∴8=
②
联立①②，得
ksinθ-8=±
，
∴ksinθ=8±
，
∴t=±
，
∴
=(8+
，
)或
=(8-
，-
)．
（2）∵向量
与向量
共线，
∴
=λ
，
∴（ksinθ-8，t）=λ（-1，2），
∴
，
∴ksinθ-8=-
，
∴t=16-2ksinθ，
∴tsinθ=（16-2ksinθ）sinθ
=-2ksin2θ+16sinθ
设sinθ=x，
∴f（x）=-2kx2+16x
=-2k（x-
）2+
，
∴
=4，
∴k=8，
sinθ=1，t=0，
∴B（8，0），
∴
•
=64．
∴
| AB |
∵
| AB |
| a |
∴-ksinθ+8+2t=0，①
∵|
| OA |
| AB |
∴8=
| (ksinθ-8)2+t2 |
联立①②，得
ksinθ-8=±
16
| ||
| 5 |
∴ksinθ=8±
16
| ||
| 5 |
∴t=±
8
| ||
| 5 |
∴
| OB |
16
| ||
| 5 |
8
| ||
| 5 |
| OB |
16
| ||
| 5 |
8
| ||
| 5 |
（2）∵向量
| AB |
| a |
∴
| AB |
| a |
∴（ksinθ-8，t）=λ（-1，2），
∴
|
∴ksinθ-8=-
| t |
| 2 |
∴t=16-2ksinθ，
∴tsinθ=（16-2ksinθ）sinθ
=-2ksin2θ+16sinθ
设sinθ=x，
∴f（x）=-2kx2+16x
=-2k（x-
| 4 |
| k |
| 32 |
| k |
∴
| 32 |
| k |
∴k=8，
sinθ=1，t=0，
∴B（8，0），
∴
| OA |
| OB |
点评：本题重点考查了平面向量的坐标运算、平面向量的基本运算等知识，属于难题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知点F是抛物线Γ：x2=2py（p＞0）的焦点，点M（x0，1）到F的距离为2．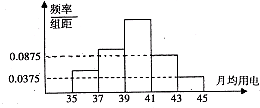
某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如图所示；其中直方图从左到右前3个小矩形的面积之比为1：2：3．该乡镇月均用电量在37～39之内的居民共有