题目内容
若a=20.5，b=logπ3，c=log2sin
，则a，b，c之间的大小关系是（ ）
| 2π |
| 5 |
| A、c＞a＞b |
| B、a＞b＞c |
| C、b＞a＞c |
| D、b＞c＞a |
考点：对数的运算性质
专题：函数的性质及应用
分析：根据指数函数、对数函数的性质分别判断它们的大小，借助于特殊值的关系比较．
解答：
解：因为a=20.5＞1，0＜b=logπ3＜1，
因0＜sin
＜1，故c=log2sin
＜0，
故选B．
因0＜sin
| 2π |
| 5 |
| 2π |
| 5 |
故选B．
点评：本题主要考查指数函数、对数函数的性质，属于基础题．
练习册系列答案
相关题目
下列命题中，正确的是（ ）
| A、a=（-2，5）与b=（4，-10）方向相同 |
| B、a=（4，10）与b=（-2，-5）方向相反 |
| C、a=（-3，1）与b=（-2，-5）方向相反 |
| D、a=（2，4）与b=（-3，1）的夹角为锐角 |
已知函数f（x）=
在（-
，+∞）上单调递减，那么实数a的取值范围是（ ）
|
| π |
| 2 |
A、（
| ||||
B、（0，
| ||||
C、[
| ||||
D、[
|
已知向量
=（8+
x，x），
=（x+1，2），其中x＞0，若
∥
，则x的值为（ ）
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| A、8 | B、4 | C、2 | D、0 |
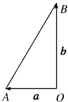
设
表示向西走10km，
表示向北走10
km，则
-
表示（ ）
| a |
| b |
| 3 |
| a |
| b |
| A、南偏西30°走20 km |
| B、北偏西30°走20 km |
| C、南偏东30°走20 km |
| D、北偏东30°走20 km |
一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”，封闭区域边界曲线的长度与区域直径之比称为区域的“周率”，下面四个平面区域（阴影部分）的周率从左到右依次记为τ1，τ2，τ3，τ4，则下列关系中正确的为（ ）
| A、τ1＞τ4＞τ3 |
| B、τ3＞τ1＞τ2 |
| C、τ4＞τ2＞τ3 |
| D、τ3＞τ4＞τ1 |
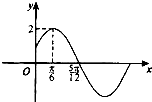已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=2sin（2x-
| ||||
D、f（x）=2sin（2x+
|
