题目内容
(1)(用综合法证明)已知△ABC的内角A、B、C所对的边分别为a,b,c,且A、B、C成等差数列,a,b,c成等比数列,证明:△ABC为等边三角形.
(2)(用分析法证明)已知a>b>c,求证:
+
≥
.
(2)(用分析法证明)已知a>b>c,求证:
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
考点:综合法与分析法(选修)
专题:综合题,不等式的解法及应用
分析:(1)先确定B的度数,再利用a、b、c依次成等比数列,及余弦定理,即可证得结论;
(2)把证明不等式转化为寻找使不等式成立的充分条件,直到使不等式成立的充分条件显然已经具备为止.
(2)把证明不等式转化为寻找使不等式成立的充分条件,直到使不等式成立的充分条件显然已经具备为止.
解答:
证明:(1)∵三内角A、B、C的度数成等差数列
∴2B=A+C,
∵A+B+C=180°,
∴B=60°,
∵a、b、c成等比数列,∴b2=ac,
∴cosB=
,
∴(a-c)2=0,∴a=c,
∵B=60°
∴△ABC为等边三角形;
(2)要证明:
+
≥
,
只要证明:[(a-b)+(b-c)][
+
]≥4,
只要证明:
+
≥2,显然成立,
∴
+
≥
.
∴2B=A+C,
∵A+B+C=180°,
∴B=60°,
∵a、b、c成等比数列,∴b2=ac,
∴cosB=
| 1 |
| 2 |
∴(a-c)2=0,∴a=c,
∵B=60°
∴△ABC为等边三角形;
(2)要证明:
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
只要证明:[(a-b)+(b-c)][
| 1 |
| a-b |
| 1 |
| b-c |
只要证明:
| b-c |
| a-b |
| a-b |
| b-c |
∴
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
点评:本题考查余弦定理,考查等差数列与等比数列的综合,解题的关键是确定角与边的关系.用分析法证明不等式,把证明不等式转化为寻找使不等式成立的充分条件,直到使不等式成立的充分条件显然已经具备为止

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x(lnx-
ax)有两个极值点,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,0) | ||
B、(0,
| ||
| C、(0,1) | ||
| D、(0,+∞) |
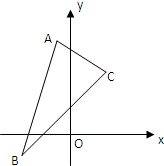 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).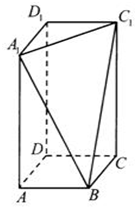 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为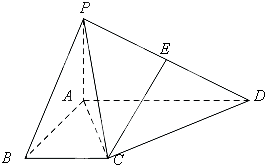 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.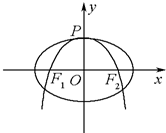 如图,抛物线C:y=-
如图,抛物线C:y=-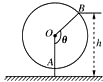 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.