题目内容

已知（1-2x）6=a0+a1x+a2x2+…+a6x6，则|a0|+|a1|+|a2|+…+|a6|=
 
．
考点：二项式定理的应用
专题：二项式定理
分析：由二项式定理可知a0，a2，a4，a6均为正数，a1，a3，a5均为负数，可得|a0|+|a1|+|a2|+…+|a6|=a0-a1+a2-a3+a4-a5+a6，把x=-1代入已知式子计数可得．
解答： 解：∵（1-2x）6=a0+a1x+a2x2+…+a6x6，
由二项式定理可知a0，a2，a4，a6均为正数，a1，a3，a5均为负数，
∴|a0|+|a1|+|a2|+…+|a6|=a0-a1+a2-a3+a4-a5+a6=（1+2）6=729
故答案为：729
点评：本题考查二项式定理，属基础题．
练习册系列答案
相关题目
函数f（x）=
1
log
1
2
x+1
的定义域为（　　）
A、（2，+∞）
B、（0，2）
C、（-∞，2）
D、（0，
1
2
）
已知“整数对”按如下规律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第58个数对是（　　）
A、（2，10）
B、（3，9）
C、（5，7）
D、（3，8）
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级12名学生某次考试成绩如下表所示：
序号123456789101112
数学成绩958580949265678498718375
物理成绩908372879171588293818663
若单科成绩85分以上（含85分），则该科成绩为优秀．
（1）根据上表完成下面的2×2列联表（单位：人）：
数学成绩优秀数学成绩不优秀合计
物理成绩优秀
物理成绩不优秀
合计
（2）根据题（1）中表格的数据计算，有多大的把握，认为学生的数学成绩与物理成绩之间有关系？（小数点后三位有效）
友情提示：随机变量K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
；
独立检验随机变量K2的临界值参考表：
P（K2≥k0）0.150.100.050.0250.0100.0050.001
k02.0722.7063.8415.0246.6357.87910.828
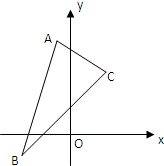已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）．
（Ⅰ）求BC边中线AD所在直线方程；
（Ⅱ）求点A到BC边的距离．
已知向量
m
=（1，
3
），单位向量
n
满足
m
•
n
=-1．
（Ⅰ）求向量
n
；
（Ⅱ）设向量
p
=（2cos2
θ
2
，cos（
π
3
-θ）），其中θ为锐角，且向量
n
与x轴平行，求|
p
-
n
|的取值范围．
已知函数f（x）=xa-
6
x
，且f（6）=5．
（1）求a的值；
（2）证明f（x）的奇偶性；
（3）判断f（x）在（1，+∞）上的单调性，并证明．
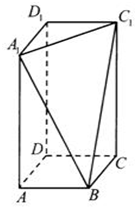在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，这个几何体的体积为
40
3
．
（1）证明：直线A1B∥平面CDD1C1；
（2）求棱A1A的长；
（3）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系． 已知点A、B的极坐标分别为（1，0）、（1，
π
2
），曲线C的参数方程为
x=rcosα
y=rsinα
（α为参数，r＞0）．
（Ⅰ）求直线AB的直角坐标方程；
（Ⅱ）若直线AB和曲线C只有一个交点，求r的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网